第一讲：课程简介

Published

February 18, 2023

这门课程将围绕两个主题展开：

在组合数学以及计算机科学中反复出现的结构（structure）、现象（phenomenon）以及问题（problem）；
能够用来尝试解决问题的基本方法与技术。

结构与问题

计数与枚举

组合数学关心的一大类问题是对组合对象的计数与枚举。比如说，计算 \(n\) 个顶点的树有多少个，或者，计算一个图有多少个匹配（matching）。那么，什么是一个好的解呢？

具有 \(n\) 个（有编号的）顶点的不同的树的个数是 \(n^{n-2}\) （Cayley公式）。
斐波那契（Fibonacci）数列是满足 \(f_0=0; f_1=1; f_n=f_{n-1}+f_{n-2}, n\ge 2\) 的一组数。可以得到它的通项是 \(f_n = \frac{1}{\sqrt{5}}\tp{\phi_1^n-\phi_2^n}\)，其中 \(\phi_1 = \frac{1+\sqrt{5}}{2}\)，\(\phi_2 = \frac{1-\sqrt{5}}{2}\)。
计算一个二分图 \(G=(V_1\cup V_2, E)\) 上的完美匹配数。假设 \(\abs{V_1}=\abs{V_2}=n\)。如果我们用 \(I\in\set{0,1}^{n\times n}\) 表示其相邻矩阵（incidence matrix），即 \(I(i,j)=1\) 当且仅当二分图左边的第 \(i\) 个顶点和右边第 \(j\) 个顶点有一条边相邻。那么 \(G\) 中完美匹配的个数为 \[ \sum_{\sigma \in S_n}\prod_{i=1}^n I(i,\sigma(i)). \]

对于计算机科学来说，我们关心的是是否有高效的算法来计算这些量，这里高效指的是多项式时间的算法。在理论计算机科学中，会专门研究问题的计数复杂性（Counting Complexity） 。

在上面三个例子中，树的个数和斐波那契数列的通项，对于每一个输入 \(n\)，显然都可以利用给出的公式快速的计算出来答案。但是对于第三个问题，假设矩阵 \(I\) 是问题的输入，是否有高效的算法依然是一个公开问题。

实际上，即使对于非常类似的问题，其计数复杂性也会有天壤之别。比如说，我们在线性代数课中学过，给定一个矩阵 \(A=(a_{ij})_{1\le i,j\le [n]}\in\^R^{n\times n}\)，如何计算其行列式（determinant）: \[ \!{det} A\defeq \sum_{\sigma\in S_n}(-1)^{N(\sigma)}\prod_{i=1}^n a_{i,\sigma(i)}. \] 我们可以使用高斯消元法在 \(O(n^3)\) 的时间内计算 \(\!{det}A\)。

这儿 \(S_n\) 是 \(n\) -元对称群，可以理解为 \(n\) 的所有置换的集合。\(N(\sigma)\) 是置换 \(\sigma\) 的逆序对的个数（见置换的奇偶性）。

我们上面第三个例子中给出的完美匹配个数的公式，实际上非常类似于行列式的定义。我们称之为积和式（permanent）： \[ \!{per} A\defeq \sum_{\sigma\in S_n}\prod_{i=1}^n a_{i,\sigma(i)}. \] Leslie Valiant 证明了，给定矩阵 \(A\)，计算 \(\!{per} A\) 是 \(\#\-{P}\)-完备的。虽然 \(\# \-P\) 和 \(\-{FP}\) 是否相等依然是公开问题，但是人们普遍相信两者是不一样的。因此大家相信这个问题不存在多项式时间的算法。

\(\-{FP}\) 即我们通常说的多项式时间可以计算的函数，它与 \(\-{P}\) 的区别是后者通常指的是判定性问题。而 \(\#\-P\) 指的是那些可以用多项式时间的非确定性图灵机的接受路径个数来表示的计算函数。

偏序结构

在组合数学和计算机科学中的一个常见结构是所谓的偏序结构。给定一个集合 \(P\) ，在上面定义的一个二元关系\(\le\subseteq U\times U\)是偏序，当且仅当其满足下面三个条件：

自反性（Reflexivity）：\(\forall x\in P\colon x\le x\)
反对称性（Antisymmetric）：\(\forall x,y\in P\colon x\le y \land y\le x\implies x=y\)
传递性（Transitivity）：\(\forall x,y,z\in P\colon x\le y \land y\le z\implies x\le z\)

我们把 \((P,\le)\) 称为一个偏序集（Partially Ordered Set）。

对于自然数 \(n\in\^N\)，我们通常使用 \([n]\) 来表示集合 \(\set{1,2,\dots,n}\)。

Figure 1: \((2^{[3]},\subseteq)\)的 Hasse 图

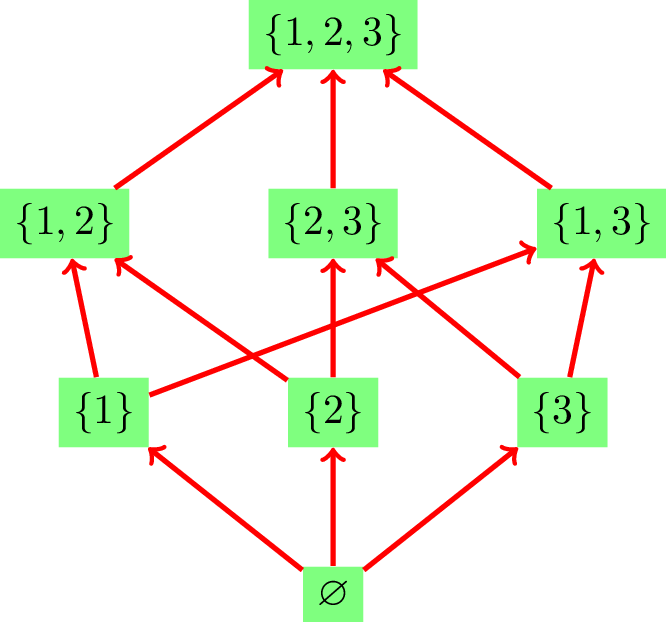
一个典型的偏序集是子集上的包含关系 \((2^{[n]},\subseteq)\)。Figure 1 是使用 Hasse 图表示的当 \(n=3\) 时候的这个集合。

我们定义一些偏序集上的概念。

Definition 1
偏序集 \((P,\le)\) 的一个子集 \(C\subseteq P\) 被称为链（chain），当且仅当其中任何两个元素都是可以比较的，即 \[ \forall x,y\in C\colon x\le y \lor y\le x. \]

比如在 Figure 1 中，\(C=\set{\emptyset, \set{1},\set{1,2},\set{1,2,3}}\) 就构成一个链。当然了，\(C\) 的任何一个子集也是一个链。一个偏序集中最长链的长度被称为这个偏序集的高度（height）。显然，Figure 1 中的偏序集的高度是\(4\)。

Definition 2
偏序集 \((P,\le)\) 的一个子集 \(T\subseteq P\) 被称为反链（anti-chain），当且仅当其中任何两个元素都是不可以比较的，即 \[ \forall x,y\in C\colon x\ne y\implies x\not\le y \land y\not\le x. \]

在 Figure 1 中，\(T=\set{\set{1},\set{2},\set{3}}\) 就是一个反链。一个偏序集中最长反链的长度被称之为这个偏序集的宽度（width）。Figure 1 中偏序集的宽度是\(3\)。

Definition 3 假设 \(C_1,C_2,\dots,C_m\) 都是偏序集 \((P,\le)\) 上的链。我们说它们构成一个链覆盖（chain cover），如果满足：

\(\bigcup_{i\in [m]} C_i = P\)，即这些链覆盖了 \(P\) 中所有元素；
\(\forall i,j\in [m]\colon i\ne j\implies C_i\cap C_j=\emptyset\)，即这些链是不相交的。

Definition 4 假设 \(T_1,T_2,\dots,T_p\) 都是偏序集 \((P,\le)\) 上的反链。我们说它们构成一个反链覆盖（antichain cover），如果满足：

\(\bigcup_{i\in [p]} T_i = P\)，即这些反链覆盖了 \(P\) 中所有元素；
\(\forall i,j\in [p]\colon i\ne j\implies T_i\cap T_j=\emptyset\)，即这些反链是不相交的。

我们后续的课程中会证明如下一个定理：

Theorem 1 (Dilworth)

任何一个偏序集的最小链覆盖的大小等于它的宽度。
任何一个偏序集中的最小反链覆盖的大小等于它的高度。

Dilworth 定理是一个典型的所谓 min-max 定理，或者被称为对偶定理。这种类型的定理在组合数学中是很多的。我们也将在后续的课程中证明其和König’s 定理以及Hall’s Marriage 定理是等价的。并且，它们在某种意义下都可以看成是线性规划的强对偶定理的推论。

极值组合学（extremal combinatorics）

任意六个人中，要么至少有三人互不相识，要么至少有三人互相认识。

用图论的语言来说，上面这个事实可以写成下面这个命题

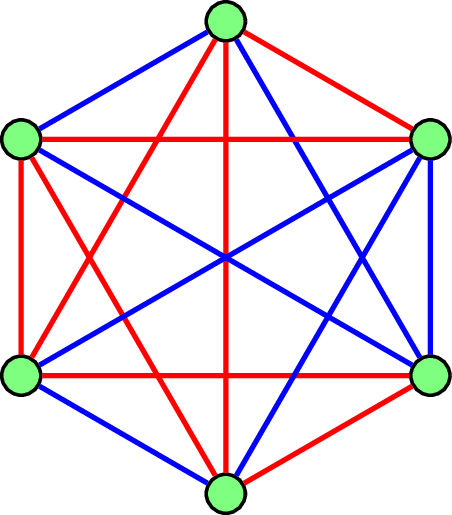
Proposition 1
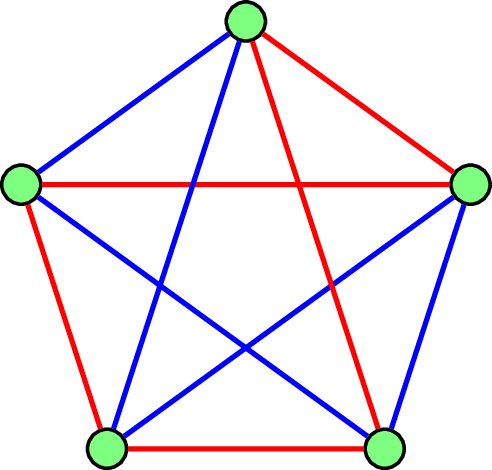
对于任何一个 \(K_6\) 的边上的红/蓝染色，要么存在一个所有边都是红色的 \(K_3\) 子图，要么存在一个所有边都是蓝色的 \(K_3\) 子图。

可以证明，存在一种对于 \(K_5\) 的边的红蓝染色，使得红色和蓝色的 \(K_3\) 都是不存在的。我们可以把上面这个现象进行推广：对于任何整数 \(r,s\ge 2\)，定义 \(R(r,s)\) 为最小的整数 \(N\)，使得任意对于 \(K_N\) 的边的红蓝染色，要么存在一个所有边都是红色的 \(K_r\) 子图，要么存在一个所有边都是蓝色的 \(K_s\) 子图。根据上面的结论，我们知道 \(R(3,3)=6\)。这个数被称为Ramsey数。

首先，我们要说明 Ramsey 数是良定义的，即是否对于任何 \(r\) 与 \(s\)，\(R(r,s)\) 都是有限数。Erdős-Szekeres 定理给了 Ramsey 数一个上界：

Theorem 2 (Erdős-Szekeres)
对于任意的 \(r,s\ge 2\), \(R(r,s)\le \binom{r+s-2}{r-1}\).

Proof.
我们只需证明关于 \(R(r,s)\) 的不等式 \[ R(r,s) \le R(r-1,s) + R(r,s-1). \] 有了这个不等式之后，Erdős-Szekeres 定理可以通过对 \(r+s\) 进行归纳来验证。

设 \(N=R(r-1,s)+R(r,s-1)\)，我们只需要证明，对于 \(K_N\)的任何一个红蓝染色中，要么存在红色 \(K_r\)，要么存在蓝色 \(K_s\)。现在固定一个染色，考察点 \(1\) 相邻的所有 \(N-1\) 条边 \(\set{1,2},\set{1,3},\dots,\set{1,N}\) 的颜色。根据鸽笼原理，要么存在至少 \(R(r-1,s)\) 条红边，要么存在 \(R(r,s-1)\) 条蓝边。

假设存在 \(R(r-1,s)\) 条红边，则这些边的除去 \(1\) 之外的端点构成的图中要么存在一个红色的 \(K_{r-1}\)，要么存在一个蓝色的 \(K_s\)。如果是后者，我们证明直接结束了；如果是前者，这个红色的 \(K_{r-1}\) 在加上顶点 \(1\) 之后就形成一个红色 \(K_r\)，亦得证。

对于存在 \(R(r,s-1)\) 条蓝边的情况，我们可以进行类似的讨论。

我们今天还会证明一个当 \(r=s\) 的时候，Ramsey 数的一个下界：

Theorem 3 (Erdős)
对于任意的 \(s\ge 3\), \(R(s,s)\ge 2^{s/2}\).

极值组合学这个学科研究很多类似 Ramsey 数风味的问题，即关心“当一个系统足够大时，某类结构一定会出现”之类的现象。这是一个很深刻的学科，它的发展也给计算机科学提供了很多数学工具。这门课里，我们不会很深入的研究这门学问，但大家将来会看到，对于 Ramsey 数的估计将成为很多我们介绍的证明技术的竞技场。

方法与技术

生成函数（generating function）

生成函数是一类非常有用的工具。考虑如下问题，计算 Fibonacci 数列 \[ 1,1,2,3,5,\dots, \] 即满足递推式 \[ f_0=1; f_1=1; \forall n\ge 2, f_n=f_{n-1}+f_{n-2} \] 的数列的通项。

为了方便之后的处理，我们可以把数列的下标扩展到所有整数，即对于 \(n<0\)，我们让 \(f_n=0\)。 \[ \dots,f_{-2}=0,f_{-1}=0,f_0=0,f_1=1,f_2=1,f_3=2,f_4=5,\dots \] 这样定义的一个好处是，我们可以写出一个对于所有 \(n\in\^Z\) 同时成立的递推式： \[ \forall n\in \^Z\colon f_n = f_{n-1}+f_{n-2}+\*1[n=1]. \tag{1}\] 我们定义一个所谓的形式级数： \[ F(z) = \sum_{n\in\^Z} f_n\cdot z^n. \] 函数 \(F(z)\) 就被称为斐波那契数列 \(\set{f_n}_{n\in\^Z}\) 的生成函数。

对于任意 \(n\in\^Z\)，我们可以对 Equation 1 的左右两边同时乘上 \(z^n\)，从而得到 \[ f_n\cdot z^n = f_{n-1}\cdot z^n+f_{n-2}\cdot z^n+\*1[n=1]\cdot z^n. \tag{2}\]

对于所有的 \(n\in\^Z\)，把 Equation 2 （在形式上）加起来，我们得到 \[ \begin{align*} &\phantom{{}\iff{}}\sum_{n\in\^Z} f_n\cdot z^n = \sum_{n\in\^Z} f_{n-1}\cdot z^n+\sum_{n\in\^Z} f_{n-2}\cdot z^n + z\\ &\iff F(z) = z\cdot F(z) + z^2 F(z) + z\\ &\implies F(z) = \frac{z}{1-z-z^2}. \end{align*} \] 接下来，我们想把 \(F(z)=\frac{z}{1-z-z^2}\) 写成多项式的形式，然后找出每一项的系数。简单的待定系数法可以得到 \[ F(z) = \frac{1}{\sqrt{5}}\tp{\frac{1}{1-\phi_1\cdot z}-\frac{1}{1-\phi_2\cdot z}}， \tag{3}\] 其中 \(\phi_1=\frac{1+\sqrt{5}}{2}\)，\(\phi_2 = \frac{1-\sqrt{5}}{2}\)。接下来，我们来计算 \(\frac{1}{1-\phi_i\cdot z}\) 的多项式展开。根据级数的知识，我们有对于 \(\abs{z}<1\)， \[ 1+z+z^2+z^3+\dots = \frac{1}{1-z}. \] 因此，对于 \(\abs{\phi z}<1\)，可以得到 \[ \frac{1}{1-\phi\cdot z} = 1+\phi\cdot z+\phi^2\cdot z^2+\phi^3\cdot z^3+\cdots \] 把这个式子代入 Equation 3，可以得到 \(F(z)\) 的多项式表示中 \(z^n\) 的系数为 \[ [z^n](F(z)) = f_n = \frac{1}{\sqrt{5}}\tp{\phi_1^n-\phi_2^n}. \]

我们这儿的处理在直观上把 \(F(z)\) 当成了数学分析中的多项式，因此，很多操作涉及到收敛性的问题。我们目前暂时对其避而不谈。实际上，关于生成函数严格的处理需要使用形式级数理论。

可以看到，使用生成函数求解递推式是一种非常通用的方法。在我们的课程中会详细的讨论它的使用。

概率法（probabilistic methods）

概率方法是在组合数学中证明存在性性质的一类重要方法。它的基本想法很简单：为了证明某个组合对象是存在的，我们定义一个可能包含这个对象的样本集，然后证明从这个样本集中进行采样的时候，有非零的概率能够得到想要的组合对象。

在这门课程中，我们会系统的学习离散空间的概率论，然后介绍概率法的一些基本想法及应用。同时，也是为下个学期学习基于测度理论的概率论做准备。

我们来使用概率法证明之前提到的 Ramsey number 的下界（Theorem 3）。

Proof.
为了证明对于 \(s\ge 3\)，\(R(s,s)\ge 2^{s/2}\)，我们只需要证明对于 \(K_N\) （\(N=2^{s/2}\)），存在一个对于其边的红/蓝二着色，使得在 \(K_N\) 不存在同色的 \(K_s\) 子图。为了证明这样一种边着色的存在性，我们考虑按照如下方式进行随机着色：每一条边独立的、等概率的着成红色或者蓝色。我们考察在这种随机着色方式下 \(K_N\) 中出现同色 \(K_s\) 子图的概率，即 \[ \Pr{\exists \mbox{ monochromatic }K_s\mbox{ subgraph in }K_N}. \] 如果我们能够证明这个概率小于 \(1\)，则能够说明，有非零的概率，能够得到一个不具有任何同色 \(K_s\) 子图的着色方案，即我们想要的组合结构存在。

我们假设 \(K_N\) 的顶点集是 \([N]\)。使用 union bound，我们有 \[ \begin{align*} &\phantom{{}={}}\Pr{\exists \mbox{ monochromatic }K_S\mbox{ subgraph in }K_N}\\ &=\Pr{\mbox{for some }S\in\binom{[N]}{s}, K_S\mbox{ is monochromatic}}\\ &\le\sum_{S\in\binom{[N]}{s}} \Pr{K_S\mbox{ is monochromatic}}\\ &=\binom{N}{s}\cdot 2\cdot 2^{-\binom{s}{2}}. \end{align*} \] 容易验证，对于 \(N=2^{s/2}\)，在 \(s\ge 3\) 的时候 \(\binom{N}{s}\cdot 2\cdot 2^{-\binom{s}{2}}<1\)。

代数方法（algebraic methods）

我们还会介绍一些使用代数方法研究组合问题的例子。考虑一个无向图 \(G=(V,E)\) 以及它的邻接矩阵 \(A_G\)。可以从线性代数的角度来研究 \(A_G\) 的性质，从而得到 \(G\) 的性质。一个经典的例子是计算图中生成树个数的基尔霍夫（Kirchhoff）定理。

在陈述定理之前，我们先定义几个记号。

Definition 5
对于无向图 \(G=(V,E)\)，其中 \(V=[n]\)，我们用 \(\!{deg}(i)\) 表示点 \(i\) 的度数。

使用矩阵 \(D_G\defeq\!{diag}(\!{deg}(1),\!{deg}(2),\dots,\!{deg}(n))\) 表示以图的度数为对角线元素的对角矩阵。我们称 \(D_G\) 为 \(G\) 的 度数矩阵。
矩阵 \(L_G\defeq D_G-A_G\) 被称为图 \(G\) 的拉普拉斯（Laplacian）矩阵，有时候简称为 \(G\) 的 Laplacian。

对于一个 \(n\times n\)的矩阵 \(A\) 以及任意的 \(i\in [n]\)，我们使用 \(A^{[-i]}\) 表示把 \(A\)的第 \(i\) 行与第 \(i\) 列删掉之后的 \((n-1)\times(n-1)\) 矩阵。类似的，对于 \(I\subseteq [n]\)，我们用 \(A^{[-I]}\) 表示把对于任意的 \(j\in I\)，矩阵 \(A\) 删掉第 \(j\) 行与第 \(j\) 列之后得到的矩阵。

Theorem 4
简单无向图 \(G([n],E)\) 的生成树个数 \(\tau(G)\) 等于 \[ \!{det} L_G^{[-j]}， \] 其中 \(j\in [n]\) 是任意一个顶点。

Proof.
我们对图的边数进行归纳。归纳起始是图只有一条边的时候，容易验证，这个时候结论是正确的。我们如下图所示定义两种减少图的边的个数的操作：删边（deletion）与缩边（contraction）：

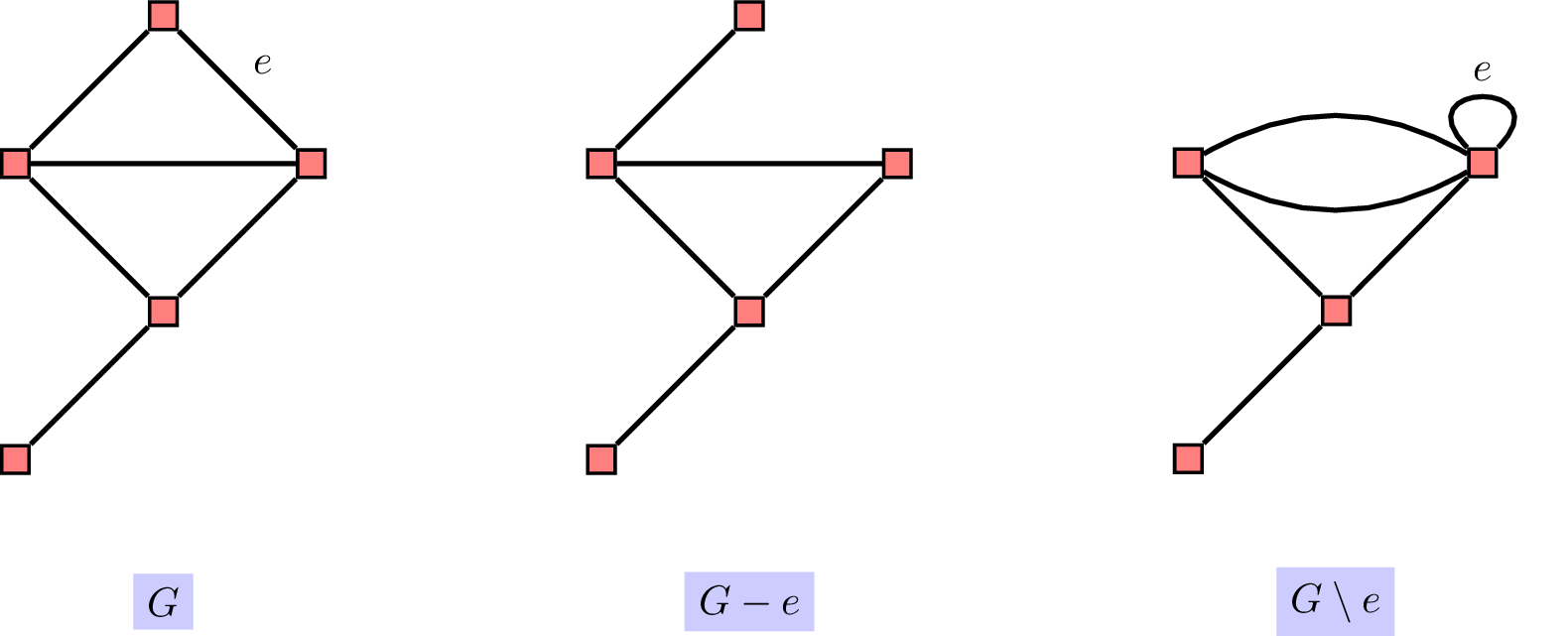
不难看出，对于图中的任何一条边 \(e\)，我们有 \[ \tau(G) = \tau(G-e) + \tau(G\setminus e). \] 我们现在来证明，对于 \(\!{det} L_G^{[-j]}\)，有同样的递推式。假设图 \(G\) 有超过一条边。不失一般性，假设 \(\set{1,2}\) 是一条边。我们来考察矩阵 \(L_G^{[-2]}\) 和矩阵 \(L_{G-\set{1,2}}^{[-2]}\)。这两个矩阵的区别来自于 \(G\) 与 \(G-\set{1,2}\) 中顶点 \(1\) 的度数。具体来说，我们有 \[ L_G^{[-2]}=L_{G-\set{1,2}}^{[-2]}+\begin{bmatrix} 1 & 0 & \cdots & 0\\ 0 & 0 & & \\ \vdots & & \ddots & \\ 0 & & & 0 \end{bmatrix}. \tag{4}\] 我们计算 \(\!{det} L_G^{[-2]}\) 可以得到 \[ \!{det} L_G^{[-2]}=\sum_{j=1}^{n-1} (-1)^{j+1}\cdot L_G^{[-2]}(1,j)\cdot \!{det} L_G^{-[1,2,j+1]}. \tag{5}\]

根据 Equation 4，Equation 5 的右边等于 \[ \!{det} L_{G-\set{2,1}}^{[-2]} + \!{det} L_G^{[-\set{1,2}]} = \!{det} L_{G-\set{2,1}}^{[-2]} + \!{det} L_{G\setminus\set{1,2}}^{[-1]}. \] 根据归纳假设 \[ \!{det} L_{G-\set{2,1}}^{[-2]} =\tau(G-\set{1,2}),\quad \!{det} L_{G\setminus\set{1,2}}^{[-1]} = \tau(G\setminus{1,2}), \] 即 \[ \!{det} L_G^{[-2]} = \tau(G-\set{1,2}) + \tau(G\setminus{1,2}) = \tau(G). \]

我们可以使用 Theorem 4 来证明之前提到的 Cayley 公式。注意到 \(n\) 个（有编号的）顶点的不同的树的个数等于 \(K_n\) 的生成树的个数。因此，其等于 \[ \!{det} L_{K_n}^{[-1]} = \!{det} \begin{bmatrix} n-1 & -1 & \cdots & -1\\ -1 & n-1 & & -1\\ \vdots & & \ddots & \vdots\\ -1 & -1 & \dots & n-1 \end{bmatrix} =n^{n-2}. \]

参考材料

我们这门课的主要参考书有：

Combinatorics: A Guided Tour, by David Mazur.
Concrete Mathematics, by Ronald Graham, Donald Knuth, Oren Patashnik
The Probabilistic Method, by Noga Alon, Joel Spencer.
A Course in Combinatorics, by Jacobus H. van Lint, Richard Wilson.