第十讲:概率法 I:概率、期望与调整法
概率法(The Probabilistic Method)的基本方法
概率法是组合数学中证明结构存在性的一类重要的技术。它的基本思路是,为了证明满足某种组合性质的结构存在,构建包括该结构的概率空间,并证明在该概率空间中具有该性质的结构出现的概率非零。我们在第一节课已经使用这个方法给出了 Ramsey 数的一个下界。今天,我们来考察更多的例子。
锦标赛图(Tournament)
给定包含 \(n\) 个顶点的有向图 \(G=(V=[n],E)\),如果对于所有的点对之间都存在一条有向边,那么我们称它为锦标赛图。其中的每一条边\((x,y)\in E\) 反映了玩家 \(x\) 和 \(y\) 之间的比赛结果,也即玩家 \(x\) 战胜玩家 \(y\)。我们接下来会定义一类以整数 \(k\) 为下标的关于锦标赛图的性质 \(P_k\),该性质要求在给定的锦标赛图中选定任意 \(k\) 个玩家,我们都可以在剩下的玩家中找到一位优胜者 \(x\),使得其战胜这 \(k\) 个玩家。更严格的说,我们可以用数学的语言将 \(P_k\) 表述为: \[ \forall S\in \binom{[n]}{k},\ \exists x\in V\setminus S \text{ s.t. }\forall y\in S,\ (x,y)\in E$ \]
接下来我们将使用概率法证明,对于给定的常数 \(k\),当 \(n\) 充分大的时候,我们总是能够找到包含\(n\)个顶点的锦标赛图,使得其满足性质 \(P_k\)。
Theorem 1 (Erdős)
对于给定常数 \(k\),当 \(\binom{n}{k}(1-2^{-k})^{n-k}<1\) 的时候,存在包含 \(n\) 个顶点的锦标赛图使得性质 \(P_k\) 成立。
Proof. 对于任意的整数 \(n\),我们定义一个包含所有锦标赛图的概率空间。具体地来说,我们令 \(\+G\) 为一个随机锦标赛图,对于其中的任意两个玩家(顶点) \(x\) 和 \(y\),我们均匀随机的选择从 \(x\) 到 \(y\) 的有向边 \((x,y)\) 或从 \(y\) 到 \(x\) 的有向边 \((y,x)\)。对于任意的大小为 \(k\) 的玩家的集合 \(S\in\binom{[n]}{k}\),我们定义随机变量 \(X_S\triangleq\*1[\forall x\in V\setminus S, \exists y\in S,(x,y)\notin E]\)。我们有 \[\begin{align*} \Pr{G\text{ does not satisfy }P_k}&=\Pr{\exists S\in \binom{[n]}{k}, X_S=1}\\ &\leq \sum_{S\in \binom{[n]}{k}}\Pr{X_S=1}\\ &=\binom{n}{k}\tp{1-2^{-k}}^{n-k}<1. \end{align*}\]
可以观察出,存在 \(n=O\tp{k^22^k}\) 满足定理的条件。
割问题(Cut)
给定一个顶点集合为 \(V=[n]\) 的无向图 \(G=(V,E)\),将图划分为 \(S\) 和 \(\ol S\triangleq V\setminus S\) 两部分。我们称两个顶点集合之间的连边 \[ E\tp{S,\ol S}\defeq\set{e\in E: e=\set{x,y},x\in S,y\in \ol S} \] 为图的一个割。
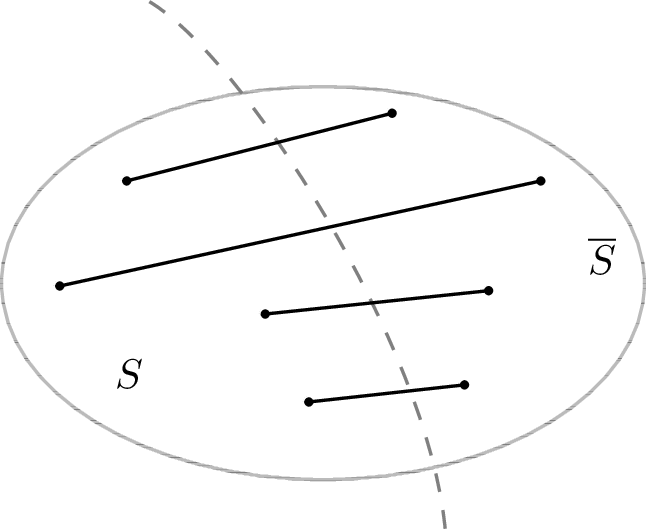
割规模下界
我们首先用概率方法说明对于任意的图,一定存在一个规模大于等于边总数一半的割。为方便起见,我们称其为非平凡割。同样地,应用概率法的前提是我们如何合适的定义出包含所有割的概率空间。根据定义,我们不难发现,一个割对应图的顶点的一个划分。这意味着随机生成原图的任意一个割等价于随机生成原图的一个顶点子集 \(S\)。令 \(\+S\) 为一个随机的点集,其中每一个顶点 \(v\in V\) 有 \(1/2\) 的概率包含进 \(\+S\)中。那么我们可以证明 \[\begin{align*} \E{\abs{E\tp{\+S,\ol{\+S}}}}=\sum_{e=\tp{i,j}\in E}\Pr{e\in E\tp{\+S,\ol{\+S}}}=\frac{1}{2}\abs{E}. \end{align*}\] 上述结果可以理解成所有割大小的平均值为总边数规模的一半,因此这说明了一定存在一个非平凡割。
概率法去随机化构造非平凡割
我们可以根据随机点集 \(\+S\) 定义一列随机变量 \((X_i=\*1[i\in \+S])_{i\in[n]}\)。那么图中的割的规模可以看成是关于随机变量 \((X_i)_{i\in[n]}\)的一个函数,也就是 \[ f\tp{X_1,X_2,\dots,X_n}=\abs{E\tp{\+S,\ol{\+S}}}. \] 由我们前面的证明,我们有 \[ \E{f\tp{X_1,X_2,\dots,X_n}}\geq \frac{\abs{E}}{2}. \] 接下来,我们将通过条件概率去随机化的方法构造一个顶点集合 \(S\),使得其对应一个非平凡割。换句话说,我们将实例化随机变量 \((X_i=x_i)_{i\in [n]}\),使得 \({f\tp{x_1,x_2,\dots,x_n}}\geq \frac{\abs{E}}{2}\)。
设 \(A\) 是一个事件,\(X\) 是一个随机变量。我们定义条件期望 \(\E{X\mid A}\) 为“在 \(A\) 发生的情况下 \(X\) 的期望”。它数学上的定义是 \[ \E{X\mid A}\defeq \sum_a a\cdot \Pr{X=a\mid A}. \]
我们应用条件期望的定义和全概率公式可以得到
\[\begin{align*} \E{f\tp{X_1,X_2,\dots,X_n}} &=\Pr{X_1=1}\E{f\tp{X_1,X_2,\dots,X_n}\mid X_1=1}+\Pr{X_1=0}\E{f\tp{X_1,X_2,\dots,X_n}\mid X_1=0}\\ &=\Pr{X_1=1}\E{f\tp{1,X_2,\dots,X_n}}+\Pr{X_1=0}\E{f\tp{0,X_2,\dots,X_n}}. \end{align*}\]
我们设置 \(X_1\) 为 \(\arg\max_{x\in\set{0,1}}\E{f\tp{x,X_2,\dots,X_n}}\) 并且按照同样的方式确定 \(X_2,\dots,X_n\) 的值。不难看出,按照这种方式构造的割是非平凡割。因此我们只需要说明,我们能够在多项式的时间内计算出 \(\arg\max_{x\in\set{0,1}}\E{f\tp{x,X_2,\dots,X_n}}\)。根据定义这件事情等价于我们固定 \(X_1\) 的值,然后剩下的顶点中随机划分。这个概率空间中割的期望的显然可以高效算出来。
调整法(Alteration)
在使用概率法的时候,我们会遇到想要的结构在概率空间中出现概率过小的情况。解决这个问题的一个方法是先得到另一个相近的结构,再通过调整来达到目的。
支配集问题(Dominating Set)
我们将要引入的例子称为支配集问题(Dominating Set)。给定一个无向图 \(G=(V,E)\) 以及一个顶点子集 \(S\subseteq V\),我们说顶点 \(V\) 被 \(S\) 支配,当且仅当对于任意一个顶点,要么它在 \(S\) 中,要么它的某个邻居在\(S\)中。
直观地来讲我们知道图的最小度数越大,那么最小支配集的规模就会越小。下面我们将会给出包含特定顶点数量的图其最小支配集的一个上界。
Theorem 2 如果无向图 \(G=(V,E)\) 的顶点最小度数为 \(\delta\),那么图中存在一个大小为 \(\frac{n\tp{1+\log(\delta+1)}}{\delta+1}\) 的支配集。
Proof. 我们来随机的生成图中的一个支配集:首先采取以下方式生成随机的顶点集合 \(\+S\subseteq V\):对于每一个顶点 \(v\in V\),我们以 \(p\) 的概率独立地将其加入 \(\+S\) 中。相应地,我们用 \(\+T\) 来表示没有被 \(\+S\) 支配的顶点的集合(即既不在 \(\+S\) 中,邻居也不在 \(\+S\) 中的点的集合)。注意到 \(\+S\cup \+T\) 一定是一个支配集。我们来计算这个支配集的期望大小。
定义随机变量 \(X=\abs{\+S}\) 和 \(Y= \abs{\+T}\)。 那 么\(\E{X}=pn\),并且根据期望的线性性, \[\begin{align*} \E{Y}&=\sum_{v\in V}\E{\*1[v\in \+T]}=\sum_{v\in V}\Pr{v\in \+T}\\ &=\sum_{v\in V}(1-p)\cdot(1-p)^{\-{deg}(v)}\leq n(1-p)^{\delta+1}. \end{align*}\] 所以我们可以得到 \(\+S\cup \+T\) 的大小的上界: \[ \E{\abs{\+S\cup \+T}}= \E{X}+\E{Y}\leq np+n\tp{1-p}^{\delta+1}.\label{eq: 1} \tag{1}\] 容易验证,Equation 1 在 \(p=\frac{\log (\delta+1)}{\delta+1}\) 时上取得最小值。此时,\(\E{\abs{\+S\cup \+T}}\leq \frac{n\tp{1+\log(\delta+1)}}{\delta+1}\)。
独立集(Independent Set)
我们可以使用类似的技巧来给出图中最大独立集大小的一个下界。先回顾一下独立集的定义。给定一个包含 \(n\) 个顶点的无向图 \(G=(V,E)\)。我们称一个顶点集合 \(S\subseteq V\) 为独立集当且仅当对于 \(S\) 中的任何一对顶点 \(u,v\in S\),\(\set{u,v}\) 不为原图中的一条边。 类似地,直观上如果一个图中包含很多边,那么图中独立集的规模会相对小。我们下面将证明,对于任意的包含特定边数的图,我们能够给出图中最大独立集的下界。
Theorem 3 对于任意大于等于 \(1\) 的常数 \(d\),如果无向图 \(G=(V,E)\) 包含 \(\frac{nd}{2}\) 条边,那么图中存在一个大小至少为 \(\frac{n}{2d}\) 的独立集。
对于图 \(G(V,E)\) 和顶点集 \(S\subseteq V\),其导出子图 \(G[S]\) 定义为 \[ G[S]\defeq \tp{S,E\cap \binom{S}{2}}. \]
Proof. 这里证明的思路还是类似地通过定义包含所有图中独立集的概率空间,然后通过分析该概率空间中的随机独立集的下界,从而证明至少存在一个和下界同样规模的独立集。同样地,我们首先采取以下方式生成随机的顶点集合 \(\+S\subseteq V\):对于每一个顶点 \(v\in V\),我们以 \(p\) 的概率独立的将其加入 \(\+S\) 中。这样得到的 \(\+S\) 并不一定是一个独立集,因为 \(\+S\) 中的顶点间可能会有边相连。因此,如果我们用 \(\+T\) 来表示集合 \(\+S\) 的导出子图\(G[\+S]\)中的边集,那么,对于 \(\+T\) 中的每一条边在 \(\+S\) 中删掉一个顶点后,剩下的一定是一个独立集。
我们定义随机变量 \(X=\abs{\+S}\) 和 \(Y= \+T\). 那么\(\E{X}=pn\) 并且 \[ \E{Y}=\sum_{e=(i,j)\in E}\Pr{i\in \+S \text{ and }j\in \+S}=\frac{p^2nd}{2}. \] 用上面方法构造的独立集大小为 \[ \E{X-Y}=np-\frac{p^2nd}{2}. \] 通过设定 \(p\) 为 \(\frac{1}{d}\),我们有 \(\E{X-Y}= \frac{n}{2d}\)。因此存在一个大小至少为 \(\frac{n}{2d}\) 的独立集。
图的围长(Girth)和染色数(Chromatic number)
Definition 1 (围长(girth))
给定一个无向图 \(G=(V,E)\),图 \(G\) 的围长定义为其最小的环所包含的边数,记作 \(\!{girth}(G)\)。特别地,当图 \(G\) 不包含任何的环,也就是说 \(G\) 是一个森林时,我们定义其围长为 \(\infty\)。
例如,对于一个二分图来说,它的围长一定是一个不小于4的偶数。
直观上来讲,围长在某种程度上反映了图的连通性。当一个图 \(G\) 越稠密,那么 \(\!{girth}(G)\) 会越小.
一个 \(q\)-合法染色指的是对于每个顶点指定 \(\set{1,2,\dots,q}\) 中的一种颜色使得所有的边上的两个顶点都被被指定的颜色都不相同。
Definition 2 (染色数(chromatic number))
一个图 \(G=(V,E)\) 的染色数被定义为最小的颜色数量 \(q\),使得图 \(G\) 包含至少一个 \(q\)-合法染色。我们通常把它记作 \(\chi(G)\)。
直观来说,稠密图的染色数会相对较大。比如对一个包含 \(n\) 个顶点的完全图 \(K_n\),它的染色数是 \(n\);而对一棵树,其染色数则为 \(2\)。然而,这种直观并不完全正确。例如,对于二分图而言,其染色数为 \(2\) 但是它可以非常稠密。事实上,Erdős 证明了存在某些图,\(\chi(G)\) 以及 \(\!{girth}(G)\) 都很大。
Theorem 4 (Erdős, 1959) 对于任意的 \(k,\ell\in \^N\),存在一个图 \(G\) 满足 \(\!{girth}(G)\geq \ell\) 并且 \(\chi(G)\geq k\)。
在这个定理的证明中,我们需要用到 Erdős–Rényi 随机图模型 \(G(n,p)\):给定 \(n\) 个顶点,对于任意一对点,我们都以概率 \(p\) 的概率独立地生成一条边。在该模型中参数 \(p\) 越大,那么生成的随机图就越稠密;反之,\(p\)越小,生成的随机图就越稀疏。通过选取合适的参数 \(p\),我们将在该模型的基础上使用概率法证明定理。
为了证明图满足要求的性质,我们可以证明存在参数\(p\),使得在\(G(n,p)\)这个模型中,各自有大于一半随机图 \(G\) 使得\(\!{girth}(G)\geq \ell\) 并且 \(\chi(G)\geq k\)。
首先我们希望选取 \(p\) 使得对于 \(G\sim G(n,p)\),有大于一半的概率 \(\!{girth}(G)\geq \ell\)。我们定义随机变量 \(X\) 为图中长度不超过 \(\ell-1\)的环的数量。因此我们只需要证明 \(\Pr{X=0}> \frac{1}{2}\) 即可。这等价于满足 \(\Pr{X\ge 1}<\frac{1}{2}\)。由马尔可夫不等式,我们有 \(\Pr{X\ge 1}\le \E{X}\)。因此,我们只需要选取合适的 \(p\) 保证 \(\E{X}< \frac{1}{2}\)。
我们接下来分析 \(\E{X}\):
\[\begin{align*} \E{X}&=\E{\sum_{i = 3}^{\ell-1}\sum_{\tp{v_1, v_2,\cdots, v_i}\atop{\forall j_1,j_2\in [i],v_{j_1}\neq v_{j_2}}} \*1 [(v_1, v_2,\cdots, v_i)\mbox{ is a cycle }]}\\ &=\sum_{i = 3}^{\ell-1}\sum_{\tp{v_1, v_2,\cdots, v_i}\atop{\forall j_1,j_2\in [i],v_{j_1}\neq v_{j_2}}} \Pr{(v_1, v_2,\cdots, v_i)\mbox{ is a cycle }}\\ &\overset{(\heartsuit)}{=}\sum_{i = 3}^{\ell-1} \binom{n}{i}\cdot\frac{i!}{2i} \cdot p^i \leq \sum_{i = 3}^{\ell-1} \frac{n(n-1)(n-2)\cdots(n-i+1)}{2i}\cdot p^i\\ &\leq \sum_{i = 3}^{\ell-1} \tp{np}^i\leq \tp{np}^{\ell}, \end{align*}\] 其中 \((\heartsuit)\) 是由于 \(i\) 个顶点可以参与构成 \(i!\) 个环并且每一个环都会被重复计算 \(2i\) 次。因此 \[\begin{align*} \Pr{X>0}=\Pr{X\geq 1}\leq \E{X}\leq \tp{np}^{\ell}. \end{align*}\] 通过选取 \(p=O(\frac{1}{n})\) 我们可以满足 \(\Pr{X>0}< \frac{1}{2}\) 的要求,换句话说我们有 \(\Pr{\-{girth}(G)\geq \ell}>\frac{1}{2}\)。
接下来我们考虑第二部分,我们希望选取合适的 \(p\) 使得对于 \(G\sim G(n,p)\),有大于一半的概率 \(\chi(G)\geq k\)。一个重要的观察是,如果一个图可以使用 \(k\) 种颜色染色,那么说明这个图的顶点可以被划分成 \(k\) 个不相交的部分(每种颜色的顶点对应一个部分),使得每个部分都是一个独立集。根据鸽笼原理,我们知道存在一个大小不小于 \(\frac{n}{k}\) 的独立集。用 \(\alpha(G)\) 来表示图 \(G\) 中最大独立集的大小,我们有 \[ \Pr{\chi(G)<k}\leq \Pr{\alpha(G)\geq \frac{n}{k}}. \]
对于\(x\in \^N\), \[\begin{align*} \Pr{\alpha(G)\geq x}&\leq \Pr{\exists S\in \binom{[n]}{x}, S \mbox{ is an independent set}}\\ &\leq \binom{n}{x}(1-p)^{\binom{x}{2}}\leq n^x\cdot e^{\frac{-px(x-1)}{2}}\\ &=\tp{ne^{\frac{-p(x-1)}{2}}}^x. \end{align*}\] 通过选取 \(p\geq \frac{3}{x}\log n\),我们有 \(\Pr{\alpha(G)\geq x}<\frac{1}{2}\),也即 \(\Pr{\chi(G)\geq k}>\frac{1}{2}\)。然而我们发现,当 \(x=\frac{n}{k}\),我们需要 \(p=\Omega\tp{\frac{\log n}{n}}\),这个和我们前面在计算围长的时候要求的 \(p=O\tp{\frac{1}{n}}\) 是违背的。
实际上,我们在第一部分要求 \(X=0\) 的要求太强了。我们用调整法来解决这个问题。最重要的观察在于,如果 \(X\) 不大(但非 \(0\)),我们可以通过删掉长度不超过 \(\ell-1\) 的环上的顶点,来得到 \(\!{girth}(G)\ge \ell\) 的图。我们选择 \(p=\frac{\log^2 n}{n}\)。那么 \[ \E{X}\leq \tp{np}^{\ell}=\tp{\log n}^{2\ell+1}=o(n). \] 因此,根据马尔可夫不等式, \[ \Pr{X\geq \frac{n}{2}}\leq \frac{\E{X}}{\frac{n}{2}}<\frac{1}{2}. \] 对于这样的 \(p\),\(\Pr{\chi(G)\geq k}>\frac{1}{2}\)。因此,我们可以找到一个图使得 \(\alpha(G)\leq \frac{n}{2k}\),并且长度不超过 \(\ell-1\) 的环的数量不超过 \(\frac{n}{2}\)。接下来我们从 \(G\) 出发构造 \(G'\):我们破坏掉 \(G\) 中的小环。对于每一个长度不超过 \(\ell-1\) 的环,我们去掉其中的一个顶点。那么由于 \(G'\) 包含至少 \(\frac{n}{2}\)个顶点以及 \(\alpha(G')\leq \alpha(G)\),我们有 \(\chi(G')\geq \frac{n}{2\alpha(G')}\geq k\)。因此,这样的图 \(G'\) 满足 \(\!{girth}(G')\geq \ell\) 并且 \(\chi(G')\geq k\)。