第十一讲：概率法 II：二阶矩方法

Published

May 14, 2023

二阶矩方法

随机变量性质及切比雪夫不等式

我们首先回顾一些常用的随机变量性质以及概率不等式。

给定两个独立的随机变量 $X,Y$，它们乘积的期望等于两个随机变量期望的乘积。

Proposition 1 任给两个独立的随机变量$X,Y$, \[ \E{X\cdot Y}=\E{X}\cdot \E{Y}. \]

Proof. \[ \begin{align*} \-{R.H.S.}&=(\sum_{x} x\cdot \Pr{X=x})\cdot (\sum_{y} y\cdot \Pr{Y=y})\\ &=\sum_{x,y} x\cdot y\cdot\Pr{X=x} \cdot \Pr{Y=y}\\ &=\-{L.H.S.} \end{align*} \]

对于任意随机变量 $X$，其二阶矩定义为 $\E{X^2}$。它的方差定义为二阶矩与期望的平方的差。 [ =-^2. ] 直观上，随机变量的方差反映了它与期望的偏离程度。我们将在接下来的切比雪夫不等式里定量的刻画这个关系。对于独立的随机变量，和的方差等于方差的和。

Proposition 2 任给两个独立的随机变量$X,Y$, \[ \Var{X+Y}=\Var{X}+\Var{Y}. \]

给定一列在整数上取值的随机变量$\set{X_n}_{n\in\^N}$，我们在之前使用概率法的例子中已经看到，如果我们想证明 \[ \Pr{X_n=0}\overset{n\to\infty}{\longrightarrow}1, \] 只需要使用马尔可夫不等式$\Pr{X_n>0}=\Pr{X_n\geq 1}\leq \E{X_n}$ 并说明 $\E{X_n}\overset{n\to\infty}{\longrightarrow} 0$ 就可以了。反过来，我们可以通过证明 $\E{X_n}\to\infty$ 来说明 $\Pr{X_n>0}\to 1$ 吗？答案是不对的。我们可以构造一下反例： [ X_n= \[\begin{cases} 0, &\mbox{w.p. }1-\frac{1}{n};\\ n^2, &\mbox{w.p. } \frac{1}{n}. \end{cases}\]

] 在这个例子中, $\E{X_n}=n\to \infty$ 但是 $\Pr{X_n>0}=\frac{1}{n}\to 0$。这个反例出现的原因是随机变量取值高概率是和其期望偏离很远的。因此，如果我们希望说明 $X_n>0$ 高概率成立，必须考察随机变量与其期望的集中程度。二阶矩方法，也就是切比雪夫不等式给出了这样一种刻画。

Theorem 1 (切比雪夫不等式（Chebyshev’s Inequality）) \[ \forall a>0,\ \Pr{\abs{X-\E{X}}\geq a}\leq \frac{\Var{X}}{a^2}. \]

Proof. 我们可以使用马尔可夫不等式证明: \[ \Pr{\abs{X-\E{X}}\geq a}=\Pr{\tp{X-\E{X}}^2\geq a^2}\leq \frac{\E{\tp{X-\E{X}}^2}}{a^2}=\frac{\Var{X}}{a^2}. \]

回到我们之前说的问题，一旦有了切比雪夫不等式，我们就能说明 \[ \Pr{X_n=0}\leq \Pr{\abs{X_n-\E{X_n}}\geq \E{X_n}}\leq \frac{\Var{X_n}}{\tp{\E{X_n}}^2}. \] 因此，如果我们想要说明 $\Pr{X_n=0}\to 0$，只需要证明 $\E{X_n^2}=\tp{1+o(1)}\tp{\E{X_n}}^2$。

随机图上的相变

图的性质 $\+P\colon G\mapsto 0\mbox{ or }1$ 指的是从图到 $0$ 或者 $1$ 的一个映射。

考虑 Erdős–Rényi 随机图 $G(n,p(n))$，其中 $p(n)\colon \^N \to[0,1]$ 是一个关于顶点个数的函数。我们称一个图性质 $\+P$ 具有相变性，如果 $\exists r\colon \^N\to[0,1]$ 使得

如果 $p(n)\ll r(n)$，$\Pr[G\sim G(n,p(n))]{G\mbox{ satisfies }P}\overset{n\to\infty}{\longrightarrow}0$；
如果 $p(n)\gg r(n)$，$\Pr[G\sim G(n,p(n))]{G\mbox{ satisfies }P}\overset{n\to\infty}{\longrightarrow}1$。

这里 $r$ 被称之为 $P$ 的阈值函数。下面我们将用二阶矩方法证明性质“一个图包含一个$K_4$”具有相变性，并且其阈值函数是 $n^{-\frac{2}{3}}$。

Theorem 2 图性质“$G$包含一个 $K_4$”具有阈值函数 $n^{-\frac{2}{3}}$。

令随机变量 $X$ 表示 $G$ 中 $K_4$ 的数量。当 $p(n)\ll n^{-\frac{2}{3}}$时，根据马尔可夫不等式，我们有 \[ \Pr[G\sim G(n,p(n))]{\mbox{$G$ contains a $K_4$}}=\Pr{X\geq 1}\leq \E{X}. \] 对于任意的图中的 $4$ 个顶点构成的集合 $S\subseteq \binom{[n]}{4}$，令 $X_S=\*1[G[S]\mbox{ is a clique}]$。那么 \[ \E{X}=\E{\sum_{S\subseteq \binom{[n]}{4}}X_s}=\binom{n}{4}\cdot p^6\leq n^4p^6=o(1). \]

另一方面，当$p(n)\gg n^{-\frac{2}{3}}$，使用切比雪夫不等式 \[ \Pr{X= 0}\leq \Pr{\abs{X-\E{X}}\geq \E{X}}\leq \frac{\Var{X}}{\tp{\E{X}}^2}=\frac{\E{X^2}-\tp{\E{X}}^2}{\tp{\E{X}}^2}. \]

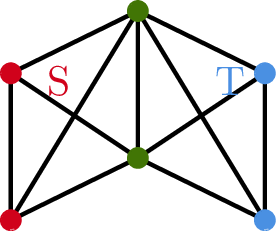
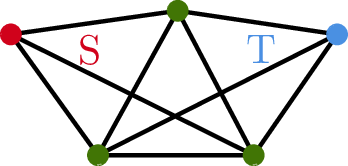
注意到 \[\begin{align*} \E{X^2}-\tp{\E{X}}^2&=\E{\tp{\sum_{S\subseteq \binom{[n]}{4}}X_s}^2}-\tp{\E{\sum_{S\subseteq \binom{[n]}{4}}X_s}}^2\\ &=2\sum_{S\neq T}\E{X_SX_T}+\sum_S \E{X_S^2}-2\sum_{S\neq T}\E{X_S}\E{X_T}-\sum_{S}\tp{\E{X_s}}^2\\ &=2\sum_{\abs{S\cap T}=2}\tp{\E{X_SX_T}-\E{X_S}\E{X_T}}+2\sum_{S\cap T=3}\tp{\E{X_SX_T}-\E{X_S}\E{X_T}}\\ &\quad+ \sum_{S}\tp{\E{X_S^2}-\tp{\E{X_S}}^2}\\ &\leq 2\sum_{\abs{S\cap T}=2}\E{X_SX_T}+2\sum_{S\cap T=3}\E{X_SX_T} + \sum_{S}\E{X_S^2}. \end{align*}\] 正如 Figure 1 所示，当 $\abs{S\cap T}=2$ 时， $X_S= X_T=1$ 当且仅当这 $11$ 条边都被包含。因此 \[ \E{X_SX_T}=\Pr{X_S=1\wedge X_T=1}=p^{11}. \] 类似地，当 $\abs{S\cap T}=3$（如 Figure 2 所示）， \[ \E{X_SX_T}=\Pr{X_S=1\wedge X_T=1}=p^9. \] 因此， \[\begin{align*} \E{X^2}-\tp{\E{X}}^2&\leq 2\sum_{\abs{S\cap T}=2}\E{X_SX_T}+2\sum_{S\cap T=3}\E{X_SX_T} + \sum_{S}\E{X_S^2}\\ &=2\binom{n}{2}\binom{n-2}{2}\binom{n-4}{2}p^{11} + 2\binom{n}{3}\binom{n-3}{1}\binom{n-4}{1}p^9\\ &\quad +\binom{n}{4}p^6\\ &\leq n^6p^{11}+n^5p^9+n^4p^6=o(\tp{\E{X}}^2). \end{align*}\] 这说明了当 $p(n)\gg n^{-\frac{2}{3}}$ 时，$\Pr{G \mbox{ contains a }K_4}\to 1$。

Weierstrass 近似定理

我们在数学分析中曾经学过，在一个闭区间上的任意一个连续的函数都可以被一个多项式函数任意地近似。我们现在使用二阶矩方法来证明这个定理。

Theorem 3 (Weierstrass近似定理) 给定一个连续函数 $f\colon [0,1]\to [-1,1]$。对于任意的 $\eps>0$ 都存在一个多项式 $p$ 满足 $\forall x\in[0,1]$, $\abs{p(x)-f(x)}\leq \eps$。

我们可以用以下的观点来看待这个问题：如 Figure 3 所示，我们从函数中选定 $n+1$ 个点，第 $i$ 个点的取值为 $f\tp{\frac{i}{n}}$。然后我们定义 \[ P_n(x)=\sum_{i=0}^n E_i(x)\cdot f\tp{\frac{i}{n}}. \] 我们希望 $E_i(x)$ 满足下列条件：

对于任意的 $x$，$\sum_{i}E_i(x)=1$。也就是说，系数是一个依赖于 $x$ 的概率分布；
对于任意的 $i,x$，$E_i(x)$ 是一个多项式；
对于任意的 $x$，系数比较集中在离 $x$ 最近的点 $\frac{i^*}{n}$ 上（$i^* = \argmin_i \abs{x-\frac{i}{n}}$）。

我们可以定义出某些随机变量来表达 $E_i(x)$，也即令 $E_i(x)=\Pr{Y=i}$。注意到我们希望当 $x$ 接近于 $\frac{i^*}{n}$ 的时候 $E_i(x)$ 很大，并且对于其他离 $x$ 比较远的点我们希望他们的系数之和比较小。考虑随机变量 $Y\sim \!{Bin}(n,x)$。我们有 $\E{Y}=nx$ 并且 $\Var{Y}=x(1-x)n\leq \frac{n}{4}$。根据切比雪夫不等式， \[ \Pr{\abs{\frac{Y}{n}-x}\geq n^{-\frac{1}{3}}}=\Pr{\abs{Y-nx}\geq n^{\frac{2}{3}}}\leq \frac{n^{-\frac{1}{3}}}{4}. \] 令 $E_i(x)=\Pr{Y=i}=\binom{n}{i}x^i(1-x)^{n-i}$。对于任意 $x\in[0,1]$， \[\begin{align*} \abs{P_n(x)-f(x)}&\leq \sum_{i=1}^nE_i(x)\abs{f\tp{\frac{i}{n}}-f(x)}\\ &=\underbrace{\sum_{i\colon \abs{i-nx}\leq n^{\frac{2}{3}}}E_i(x)\abs{f\tp{\frac{i}{n}}-f(x)}}_A + \underbrace{\sum_{i\colon \abs{i-nx}> n^{\frac{2}{3}}}E_i(x)\abs{f\tp{\frac{i}{n}}-f(x)}}_B. \end{align*}\] 由于函数 $f$ 是连续的，那么存在 $\delta$ 使得 $\forall \abs{x-y}<\delta$，$\abs{f(x)-f(y)}<\frac{\eps}{2}$。当 $n^{-\frac{1}{3}}<\delta$，我们有 $A\leq \frac{\eps}{2}$。同时，当 $n^{-\frac{1}{3}}<\eps$时，$B\leq 2\sum_{i\colon \abs{i-nx}> n^{\frac{2}{3}}}E_i(x)\leq \frac{n^{-\frac{1}{3}}}{2}\leq \frac{\eps}{2}$。因此，选定 $n\geq \max\set{\frac{1}{\eps^3},\frac{1}{\delta^3}}$，对于所有$x\in[0,1]$，我们有$\abs{P_n(x)-f(x)}\leq \eps$。