第二讲:基本计数法,组合证明,容斥原理
基本计数法:箱子与球的模型
我们考察一个把 \(k\) 个球扔到 \(n\) 个箱子里的场景,并尝试数一下有多少种不同的扔球方案。我们可以区分箱子或者球是否是相等的,以及对每一个箱子中能放多少个球给出不同的要求。很多常见组合计数问题都可以用这个模型来表示。表格 Table 1 给出了十二种不同的可能设定,它被称为 Rota’s Twelvefold Ways。

| 每个箱子允许多少个球? | ||||
|---|---|---|---|---|
| 球的种类 | 箱子的种类 | 无限制 | \(\le 1\) | \(\ge 1\) |
| 不同 | 不同 | ① | ② | ③ |
| 相同 | 不同 | ④ | ⑤ | ⑥ |
| 不同 | 相同 | ⑦ | ⑧ | ⑨ |
| 相同 | 相同 | ⑩ | ⑪ | ⑫ |
我们来看看如何填这个表。
① \(k\) 个不同的球,\(n\) 个不同的箱子
对于每一个球,把它扔到哪一个箱子有 \(n\) 种选择,因此,总共有 \(n^k\) 种方案数。
② \(k\) 个不同的球,\(n\) 个不同的箱子,要求每个箱子最多一个球
第一个球有 \(n\) 种选择,第二个球有 \(n-1\) 种选择,…,第 \(k\) 个球有 \(n-k+1\) 种选择。以此,总共有 \(n\cdot (n-1)\cdot (n-2)\cdots (n-k+1)\) 种选择。我们把这个数记作 \((n)_k\)。
\[ (n)_k\defeq n\cdot (n-1)\cdots (n-k+1) \]
⑤ \(k\) 个相同的球,\(n\) 个不同的箱子,要求每个箱子至多有一个球
这个问题等价于从 \(n\) 个箱子中选出 \(k\) 个来,每一个放一个球。因此方案数为 \(\binom{n}{k}=\frac{n!}{k!(n-k)!}\)。
④ \(k\) 个相同的球,\(n\) 个不同的箱子
这个问题相当于从 \(n\) 个箱子中选 \(k\) 个,但是允许重复选择,问有多少方案。我们把这个数称为大小为 \(k\) 的多重集(multiset)的个数,并记作 \(\multiset{n}{k}\)。我们下面来寻找 \(\multiset{n}{k}\) 的表达式。
我们构造一个所有的多重集到长度为 \(n+k\) 的 \(0\)-\(1\) 串 \(\set{0,1}^{n+k}\) 的某个子集的一个双射。实际上,给定一个以 \(1\) 结尾并且有 \(n\) 个 \(1\) 和 \(k\) 个 \(0\) 的 \(0\)-\(1\) 串可以解释成如下一个多重集:每一个 \(1\) 表示一个元素;第 \(i\) 个 \(1\) 前面的连续的 \(0\) 的个数表述第 \(i\) 个元素在多重集里选了多少个。显然,这是一个满足我们要求的双射。因此大小为 \(k\) 的多重集的个数是 \(\binom{n+k-1}{n-1} = \binom{n+k-1}{k}\),即 \(\multiset{n}{k}=\binom{n+k-1}{k}\)。
⑥ \(k\) 个相同的球,\(n\) 个不同的箱子,要求每个箱子至少一个球
可以先在每个箱子预先放一个球,然后转变为④。因此,方案数为 \[ \multiset{n}{k-n} = \binom{k-1}{k-n} = \binom{k-1}{n-1}. \]
⑨ \(k\) 个不同的球,\(n\) 个相同的箱子,要求每个箱子至少一个球
这个这个等价于求把一个大小为 \(k\) 的集合分成正好 \(n\) 组的方案数。这个数叫做第二类斯特林数(Stirling number of second kind)。我们把这个数记做 \(\stirlingII{k}{n}\)。我们会在之后讨论它的性质。
③ \(k\) 个不同的球,\(n\) 个不同的箱子,要求每个箱子至少一个球
这个问题等价于计算 \([k]\to [n]\) 的满射的个数。因此,我们可以先把 \([k]\) 分成 \(n\) 个子集,再把这 \(n\) 个子集和 \([n]\) 一一对应。所以方案个数为 \(n!\cdot\stirlingII{k}{n}\)。
⑦ \(k\) 个不同的球,\(n\) 个相同的箱子
这个问题等价于计算有多少种方案可以把 \([k]\) 分成不超过 \(n\) 个集合。因此,这个数量是 \(\sum_{i=1}^n \stirlingII{k}{i}\)。
⑫ \(k\) 个相同的球,\(n\) 个相同的箱子,要求每个箱子至少一个球
这个问题等价于问把整数 \(k\) 写成 \(n\) 个正整数之和,有多少种写法。我们把这个数记做 \(P(k,n)\)。和斯特林数一样,我们会在之后研究它的性质。
⑩ \(k\) 个相同的球,\(n\) 个相同的箱子
这个问题相当于问把整数 \(k\) 写成不超过 \(n\) 个正整数之和,有多少种写法。所以这个方案数为 \(\sum_{i=1}^n P(k,i)\)。
⑧ \(k\) 个不同的球,\(n\) 个相同的箱子,每个箱子不超过一个球
这个完全取决于 \(k\) 是否大于 \(n\),因此方案数是 \(\*1[k\le n]\)。
⑪ \(k\) 个相同的球,\(n\) 个相同的箱子,每个箱子不超过一个球
同样,这个完全取决于 \(k\) 是否大于 \(n\),因此方案数是 \(\*1[k\le n]\)。
| 每个箱子允许多少个球? | ||||
|---|---|---|---|---|
| 球的种类 | 箱子的种类 | 无限制 | \(\le 1\) | \(\ge 1\) |
| 不同 | 不同 | \(n^k\) | \((n)_k\) | \(n!\cdot\stirlingII{k}{n}\) |
| 相同 | 不同 | \(\multiset{n}{k}\) | \(\binom{n}{k}\) | \(\multiset{n}{k-n}\) |
| 不同 | 相同 | \(\sum_{i=1}^n \stirlingII{k}{i}\) | \(\*1[k\le n]\) | \(\stirlingII{k}{n}\) |
| 相同 | 相同 | \(\sum_{i=1}^n P(k,i)\) | \(\*1[k\le n]\) | \(P(k,n)\) |
组合证明
从上面球和箱子的计数问题可以看出,组合数的式子往往能和扔球的方案数对应上。这便启发我们在某些场合可以更方便的使用组合解释来证明一些恒等式或者不等式。我们今天来看一些例子,大部分例子都是通过数两遍(double counting)技巧来证明的。
Proposition 1 \[ \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}. \]
Proof. 左边是从 \(n\) 个箱子中选 \(k\) 个的方案数。右边是说这些方案可以根据是否选了 \(1\) 号箱子分成两类。如果选了 \(1\) 号,那么方案数是 \(\binom{n-1}{k-1}\),如果没有选 \(1\) 号,那么方案数是 \(\binom{n-1}{k}\)。
Proposition 2 \[ \multiset{n}{k} = \multiset{n}{k-1} + \multiset{n-1}{k}. \]
Proof. 左边是从 \(n\) 个箱子中允许重复的选 \(k\) 个的方案数。右边同样是按照是否选了 \(1\) 号箱子进行分类。
Proposition 3 (Vandermonde’s Formula) \[ \forall m,n,k>0, \quad \sum_{j=0}^k \binom{m}{j}\binom{n}{k-j} = \binom{m+n}{k}. \]
Proof. 右边是从 \(m\) 个男孩 \(n\) 个女孩中选出 \(k\) 个人,左边是枚举这选出来的 \(k\) 个人中有多少个男孩。
Proposition 4 \[ \stirlingII{n}{k} = \stirlingII{n-1}{k-1} + k\cdot \stirlingII{n-1}{k}. \]
Proof. 左边是第二类斯特林数,即把集合 \([n]\) 分成 \(k\) 个部分有多少方案。右边是说分类讨论是否 \(\set{1}\) 作为一个单独的部分被选了出来。如果是的,那只需把剩下的 \(n-1\) 个数分成 \(k-1\) 个部分。如果不是,那我们先把除掉 \(1\) 之外的 \(n-1\) 个数分成 \(k\) 个部分,然后再选一个把 \(1\) 加进去。
Proposition 5 \[ \stirlingII{n}{k} = \sum_{j=0}^{n-1}\binom{n-1}{j}\cdot\stirlingII{n-j-1}{k-1}. \]
Proof. 左边是第二类斯特林数,右边表示分情况讨论 \(1\) 所在的集合里,除了 \(1\) 之外还有多少个元素。
Proposition 6 \[ P(n,k) = P(n-1,k-1) + P(n-k,k). \]
Proof. 左边 \(P(n,k)\) 表示把整数 \(n\) 拆成 \(k\) 个正整数之和(不考虑顺序)有多少种不同的方案。右边则是分类考虑最小的数是不是 \(1\)。如果是 \(1\),我们只需把考虑把 \(n-1\) 分成 \(k-1\) 个数之和,即 \(P(n-1,k-1)\);如果不是,我们则可以把每一个数都减去 \(1\),这样每一种合法的方案都对应于把 \(n-k\) 分成 \(k\) 个正数之和的方案。
Proposition 7 \[ P(n,k) = \sum_{j=0}^k P(n-k,j). \]
Proof. 右边即枚举方案中有多少个非 \(1\) 的数。
容斥原理 (Principle of Inclusion-Exclusion)
我们想计算 \(\set{1,2,\dots,100}\) 中,有多少个数不能被 \(2,3,5\) 中的任意一个整除。分别用 \(A_2=\set{2,4,\dots,100}\),\(A_3=\set{3,6,9\dots,99}\),\(A_5=\set{5,10,\dots,100}\) 表示 \([100]\) 中所有能够被 \(2\)、\(3\)、\(5\) 整除的数;则需要计算的是 \[ \abs{\ol A_2 \cap \ol A_3 \cap \ol A_5}. \]
\(\ol A\) 表示集合 \(A\) 在 \([100]\) 中的补集,即 \(\ol A\defeq [100]\setminus A\)。
这些集合的关系可以用 Figure 1 所示的韦恩图(venn diagram)清楚的表示出来。通过这个图,我们可以知道:
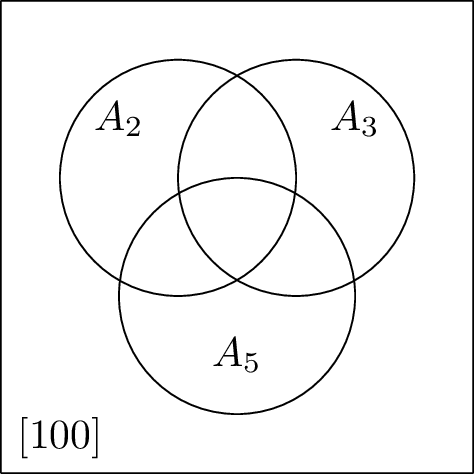
\[ \begin{align*} \abs{\ol A_2 \cap \ol A_3 \cap \ol A_5} &= 100 - \abs{A_2} - \abs{A_3}-\abs{A_5}\\ &\quad + \abs{A_2\cap A_3} + \abs{A_2\cap A_5} + \abs{A_3\cap A_5}\\ &\quad -\abs{A_2\cap A_3\cap A_5} &=100-50-33-20+16+10+6-3\\ &=26. \end{align*} \] 这种计算方法便是容斥原理。
一般来说,容斥原理用来计算在一个大的集合 \(U\) 中,我们想要的某些“好的元素”的个数。我们通常用来指定一些“坏元素”的集合 \(A_1,A_2,\dots,A_m\)。一个元素是好元素当且仅当其不在任意一个 \(A_i\) 里面。因此,我们想要计算 \(\abs{\bigcap_{i\in [m]} \ol A_j}\)。
我们引入一个直观的记号。设 \(\@A = \set{A_1,\dots,A_m}\) 为所有坏元素集合的集合。对于任意 \(J\subseteq \@A\),我们定义 \[ N_=(J) = \abs{\set{x\in U\cmid (\forall A\in J\colon x\in J) \land (\forall B \in \@A\setminus J\colon x\not\in B)}}. \] 换句话说,\(N_=(J)\) 中的元素就是那些属于 \(J\) 中的每一个集合,并且不属于 \(\@A\setminus J\) 中的每一个集合的元素。这个下标 \(=\) 的意思就是 \(J\) 正好刻画了我们要求哪些坏集合包含 \(x\),哪些坏集合不包含 \(x\)。我们类似的定义 \[ N_\ge (J) = \abs{\set{x\in U\cmid \forall A\in J\colon x\in A}}. \] 即 \(N_\ge (J)\) 中的元素就是那些属于 \(J\) 中的每一个集合的元素。和 \(N_= (J)\) 不同的是,我们对这些元素是否在 \(\@A\setminus J\) 包含的这些集合中不作要求。在很多问题中,\(N_\ge(J)\) 往往比 \(N_=(J)\) 要容易计算。在我们上面的例子中,假设 \(J=\set{A_2,A_3}\),那么 \(N_=(J)\) 就是那些能被 \(2\) 和 \(3\) 整除,但是不能被 \(5\) 整除的数。而 \(N_\ge (J)\) 则是那些能被 \(2\) 和 \(3\) 整除的数。显然,\(\abs{\bigcap_{i\in [m]} \ol A_j} = N_=(\emptyset)\)。
Theorem 1 (容斥原理)
\[
N_=(\emptyset) = \sum_{J\subseteq \@A} (-1)^{\abs{J}}N_\ge(J) = \sum_{j=0}^m (-1)^j \sum_{J\in\binom{\@A}{j}} N_\ge(J).
\]
Proof.
注意到 \(N_=(\emptyset)=|\bigcap_{i=1}^m \overline{A}_i|\),\(N_{\geq}(J)=|\bigcap_{A\in J}A|\)。我们只需要证明 \[
\abs{\bigcap_{i=1}^m \overline{A}_i}=\sum_{J\subseteq \@A} (-1)^{\abs{J}}\abs{\bigcap_{A\in J}A}.
\]
首先,对于每一个出现在 \(\bigcap_{i=1}^m \overline{A}_i\) 中的元素 \(x\),它在等式右边只会在 \(J = \emptyset\) 时被计一次。
其次,假设某个 \(x\) 在某一些 \(A_i\) 中出现了,那么它就不会在等式的左边被计数。我们可以不失一般性的假设 \(x\in A_1\cap \dots \cap A_t\)。根据二项式定理,它在右式被统计的次数为 \[ \sum_{J\subseteq\{A_1,A_2,\dots,A_t\}}(-1)^{|J|}=\sum_{j=0}^t\binom{n}{j}(-1)^j=0. \]
Example 1 (无不动点置换之个数) 假设 \(f:[n]\to [n]\) 是 \([n]\) 的一个置换。对于 \(i\in [n]\),我们说 \(i\) 是置换 \(f\) 的不动点当且仅当 \(f(i)=i\)。用 \(A_i\) 表示那些所有以 \(i\) 为不动点的置换的集合。设 \(\@A=\set{A_1,A_2,\dots,A_n}\)。那么所有没有不动点的置换的数量就是 \(N_=(\emptyset)\)。由容斥原理,我们有 \[ \begin{align*} N_=(\emptyset) & = \sum_{J\subseteq \@A}(-1)^{|J|}N_{\ge}(J)\\ & = \sum_{j=0}^n \sum_{ J \in \binom{\@A}{j} }(-1)^{j} N_{\geq}(J)\\ & = \sum_{j=0}^n \binom{n}{j}(-1)^j(n-j)!\ . \end{align*} \]
我们来求解第二类斯特林数 \(\stirlingII{n}{k}\) 的通项公式。
Example 2 (第二类斯特林数通项) 假设我们现在有 \(n\) 个不同的球和 \(k\) 个不同的箱子。根据我们上面对于 twelvefold ways 的研究,③表示的是 \([n]\to [k]\) 的满射的个数,并且该个数为 \(k!\cdot\stirlingII{n}{k}\)。我们可以用另外一种方式来计算这个数量,即使用容斥原理从 \([n]\to [k]\) 的映射中“筛去”那些不是满射的。对每一个 \(i\in [k]\),设 \(A_i=\set{f\mid f^{-1}(i)=\emptyset}\)。所有坏元素的集合的集合为 \(\@A=\set{A_1,\dots,A_k}\)。那么所有的满射的个数即为 \(N_=(\emptyset)\)。由容斥原理 \[ \begin{align*} N_=(\emptyset) & = \sum_{J\subseteq \@A}(-1)^{|J|}N_{\ge}(J)\\ & = \sum_{j=0}^k \sum_{ J \in \binom{\@A}{j} }(-1)^{j} N_{\geq}(J)\\ & = \sum_{j=0}^k \binom{k}{j}(-1)^j(k-j)^n\ . \end{align*} \] 因此,我们有 \[ \stirlingII{n}{k}=\frac{1}{k!}\sum_{j=0}^k(-1)^j\binom{k}{j}(k-j)^n. \]
回忆我们在上节课提到过在二分图中计算其完美匹配个数的问题。它可以表示成一个 \(0\)-\(1\) 矩阵 \(A\) 的积和式: \[ \!{perm} A=\sum_{\sigma\in S_n}\prod_{i=1}^n A_{i,\sigma(i)} \] 我们提到过,计算 \(\!{perm} A\) 是 \(\#\-P\) 困难的。实际上,根据 \(\!{perm} A\) 的定义式进行计算需要 \(O(n\times n!)\) 的时间。而我们可以使用容斥原理把得到一个 \(2^{O(n)}\) 时间的算法。
Theorem 2 (Ryser 公式) \[ \!{perm} A=\sum_{I\subseteq [n]}(-1)^{|I|}\prod_{i=1}^n \tp{\sum_{j\in[n]\setminus I}A_{i,j}}. \]
Proof. 设 \(U\) 为所有满足对于任意 \(i\in [n], A_{i,\sigma(i)}=1\) 的从 \([n]\) 到 \([n]\) 的映射 \(\sigma\)。对于每一个 \(i\in [n]\),设 \(A_i=\set{f\in U\mid f^{-1}(i)=\emptyset}\) 且令 \(\@A=\set{A_1,\dots,A_n}\)。根据容斥原理,图中完美匹配的个数为 \[ N_=(\emptyset)=\sum_{J\subseteq \@A}(-1)^{|J|}N_{\geq }(J) =\sum_{S\subseteq[n]}(-1)^{|S|}\prod_{i=1}^n\tp{\sum_{j\in[n]\setminus S}A_{i,j}}. \]
在计算复杂性理论中,有一个所谓的“计数版本指数时间假设(\(\#\) Exponential Time Hypothesis, \(\#\*{ETH}\))”,即假设对于 \(n\) 个变量的布尔公式可行解进行计数不存在 \(2^{o(n)}\) 时间的算法。Rado Curticapean 证明了下面定理
Theorem 3 假设 \(\#\*{ETH}\) 成立, 那么 \(\!{perm} A\) 不存在 \(2^{o(n)}\) 时间的算法。
这意味着在 \(\#\*{ETH}\) 成立的情况下,使用 Ryser 公式计算 \(\!{perm} A\) 在渐进的意义下是最优的。