第三讲：生成函数（I）

Published

March 5, 2023

\[ \require{enclose} \newcommand{circled}[1]{\enclose{circle}{#1}} %\enclose{circle}{\kern .06em 1\kern .06em} \]

一个找钱的问题

假设存在\(1\)元、\(5元\)、\(10\)元、\(20\)元面值的不限量的钞票。有多少种方法可以兑换\(30\)元？或者更一般的，有多少种方法可以兑换\(N\)元？

如果我们只使用\(1\)元钞票，我们可以按照如下方法列出所有它能组成的面值： \[ A = \emptyset + \circled{1} + \circled{1}\circled{1} + \circled{1}\circled{1} \circled{1} + \cdots. \] 我们把同样面值的钱的张数放到指数上，就可以把 \(A\) 写成： \[ A= \emptyset + \circled{1} + \circled{1}^{2} + \circled{1}^{3} +\cdots. \]

我们使用 \(\emptyset\) 表示 \(0\) 元钱。两个连续的 \(\circled{1}\) 表示我们摆出两张 \(1\) 元来合成 \(2\) 元，以此类推。

如果我们使用面值为 \(1\) 元和 \(5\) 元的钞票，能够组成的面值为： \[ \begin{align*} B &= \emptyset + \circled{5}A + \circled{5}^{2}A + \circled{5}^{3}A + \cdots =\tp{\emptyset + \circled{5} + \circled{5}^{2} + \circled{5}^{3} +\cdots}A. \end{align*} \]
类似的，使用 \(1\) 元、\(5\) 元和 \(10\) 元，我们可以组成： \[ C = \tp{\emptyset + \circled{10} + \circled{10}^{2} + \circled{10}^{3} +\cdots}B. \]
如果使用所有 \(1\) 元、\(5\) 元、\(10\) 元和 \(20\) 元面值，我们可以得到：

\[ \begin{align*} D&= \tp{\emptyset + \circled{20} + \circled{20}^{2} + \circled{20}^{3} +\cdots}C\\ &=\tp{\emptyset + \circled{20} + \circled{20}^{2} + \circled{20}^{3} +\cdots}\cdot \tp{\emptyset + \circled{10} + \circled{10}^{2} + \circled{10}^{3} +\cdots}\\ &\quad \cdot \tp{\emptyset + \circled{5} + \circled{5}^{2} + \circled{5}^{3} +\cdots}\cdot \tp{\emptyset + \circled{1} + \circled{1}^{2} + \circled{1}^{3} +\cdots}. \end{align*} \]

我们用一个变量 \(z\) 来表示 \(\circled{1}\)，并且分别用 \(z^5\)、\(z^{10}\)、\(z^{20}\) 来表示 \(\circled{5}\)、\(\circled{10}\) 与 \(\circled{20}\)。则有 \[\begin{align*} D&=\tp{1 + z^{20} + z^{40} + z^{60} + \cdots}\cdot\tp{1 + z^{10} + z^{20} + z^{30} + \cdots}\\ &\quad \cdot\tp{1+ z^5 + z^{10} + z^{15} +\cdots}\cdot \tp{1+ z + z^2 + z^3 +\cdots}. \end{align*}\]

在多项式 \(D\) 中 \(z^{30}\) 的系数 \([z^{30}] D\) 即用这几种面值的钞票兑换 \(30\) 元的方案的种数。当 \(\abs{z}<1\) 的时候，\(D\) 是一个收敛的级数，满足

对于多项式 \(f(z) = \sum_i a_i z^i\) 及 \(n\in\^N\)，我们使用 \([z^n]f(z)\) 来表示 \(f(z)\) 中 \(z^n\) 的系数，即 \(a_n\)。

\[ D=\frac{1}{(1-z)(1-z^{5})(1-z^{10})(1-z^{20})}. \] 因此，对于任意的 \(m\in\^N\)，我们可以使用泰勒级数计算\([z^m]D\)，即 \([z^m]D(z) =\frac{D(z)^{(m)}}{m!}\vert_{z=0}\)。

生成函数的定义

我们在上个例子中得到的多项式 \(D(z)\) 即为找钱方案数的生成函数。

Definition 1 (普通生成函数) 给定数列 \(\set{a_n }_{ n\geq 0 }\)，它对应的普通生成函数（ordinary generating function）为 \(A(z)=\sum_{n\geq 0}a_nz^n\)。

在本门课的大部分场合，我们都可以把 \(A(z)\) 理解成一个多项式函数。但实际上，这儿的 \(A(z)\) 是所谓的形式级数，它在 \(z\) 的收敛半径内有着和多项式类似的运算法则（因此，本门课大部分的时候我们直接把 \(A(z)\) 当成收敛的级数来处理。这当然是不严格的，但在我们遇到的例子上并没有问题。）。我们不会严格的讨论形式级数，关于其理论，大家可以参看生成函数领域的名著 generatingfunctionology 的第二章。这是一本非常有趣的书，值得每一个人阅读。

我们来看几个常见的生成函数例子：

\(a_k = 1\)。则 \[ A(z)=1 + z + z^{2} + \cdots = \frac{1}{1 - z} \tag{1}\]
\(a_k = \binom{n}{k}\)。根据二项式定理， \[ A(z)={n\choose 0} + {n\choose 1}z + {n \choose 2}z^2 + \cdots =\sum_{k\geq 0}{n \choose k}z^k = (1+z)^n \tag{2}\]
\(a_k = \multiset{n}{k} = \binom{n + k - 1}{k}\)。则有 \[ A(z)=\multiset{n}{0} + \multiset{n}{1}z + \cdots = \sum_{k\geq0}\multiset{n}{k}z^k = \frac{1}{(1-z)^n} \tag{3}\] Equation 3 可以用泰勒级数直接验证。我们这儿给它一个组合证明。\(\multiset{n}{k}\) 表示的是往 \(n\) 个不同的箱子里放 \(k\) 个相同的球的方案数。我们可以考虑枚举每一个箱子放的球数，从而得到它的生成函数为 \[ A(z) = (1+z+z^2+\dots)^n = \frac{1}{(1-z)^n}. \]

我们接着来看几个对生成函数的基本操作。假设存在两个生成函数 \(F(z)=\sum_{k\geq 0}f_kz^k\) 与 \(G(z) = \sum_{k\geq0}g_kz^k\)。我们有如下运算法则：

\([z^k](F+G) = f_k + g_k\);
\([z^k](z^mF) = f_{k-m}\);
\([z^k](c\cdot F) = cf_k\);
\([z^k](F') = (k+1)f_{k+1}\).

使用这些基本的级数的生成函数以及上述几个操作，我们就能够得到很多新的生成函数。

应用

斐波那契数列的通项

我们在第一讲中已经讨论过斐波那契数列：

\(f_0 = 0, f_1 = 1\);
\(\forall n \geq 2, f_n = f_{n-1}+f_{n-2}\).

我们在这儿重复一次使用生成函数求解其通项的过程。它对应的生成函数是 \[ F(z)=f_0+f_1z+f_2z^2+f_3z^3+f_4z^4+\cdots. \]

如果我们对所有的 \(i\in \^N\)，令\(f_{-i}=0\)，则可以得到一个递推式 \[ \forall n\in \^Z\colon f_n = f_{n-1}+f_{n-2}+\*1[n=1]. \tag{4}\]

对于任意 \(n\in\^Z\)，我们可以对 Equation 4 的左右两边同时乘上 \(z^n\)，从而得到 \[ f_n\cdot z^n = f_{n-1}\cdot z^n+f_{n-2}\cdot z^n+\*1[n=1]\cdot z^n. \tag{5}\]

对于所有的 \(n\in\^Z\)，把 Equation 5 加起来，我们得到 \[ \begin{align*} &\phantom{{}\iff{}}\sum_{n\in\^Z} f_n\cdot z^n = \sum_{n\in\^Z} f_{n-1}\cdot z^n+\sum_{n\in\^Z} f_{n-2}\cdot z^n + z\\ &\iff F(z) = z\cdot F(z) + z^2 F(z) + z\\ &\implies F(z) = \frac{z}{1-z-z^2}. \end{align*} \]

因此，我们只需计算 \([z^n]\tp{\frac{z}{1 - z - z^2}}\)。我们的目标是把 \(\frac{z}{1 - z - z^2}\) 表示成一些基本级数的和。设 \[ F(z) = \frac{z}{1 - z - z^2} = \frac{A}{1 - c_1 z} + \frac{B}{1 - c_2 z}, \] 其中 \(c_1\)、\(c_2\)、\(A\)、\(B\) 均是待定常数。注意到方程 \(1-z-z^2=0\) 的两个根分别是 \(z_1=-\frac{1+\sqrt 5}{2}\) 和 \(z_2=-\frac{1-\sqrt 5}{2}\)，我们可以计算出 \(c_1 = \frac{1 + \sqrt{5}}{2}\) 且 \(c_2 = \frac{1 - \sqrt{5}}{2}\)。因此，通过求解方程组 \[\begin{align*} \left\{ \begin{aligned} &A + B = 0 \\ &Ac_2 + Bc_1 = -1 \end{aligned} \right. \end{align*}\] 可以得到 \(A = \frac{1}{\sqrt 5}\)，\(B = -\frac{1}{\sqrt 5}\)。因此 \[ f_n = [z^n]\tp{\frac{z}{1 - z - z^2}} = \frac{1}{\sqrt{5}}\tp{\left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n}。 \]

从上面的例子，我们可以总结出一个求解递推式的“套路”：

写出一个对于任意 \(n\in\^Z\) 成立的递推式；
对递推式的两边乘上 \(z^n\)，然后对所有的 \(n\in Z\) 求和；
使用各种技巧把上式写成一个关于 \(F(z)\) 的方程并解出 \(F(z)\)；
读出 \(F(z)\) 的系数。

上述步骤的实施有时候需要一些技巧，我们通过研究更多的例子来进行讨论。

扇形图上的生成树

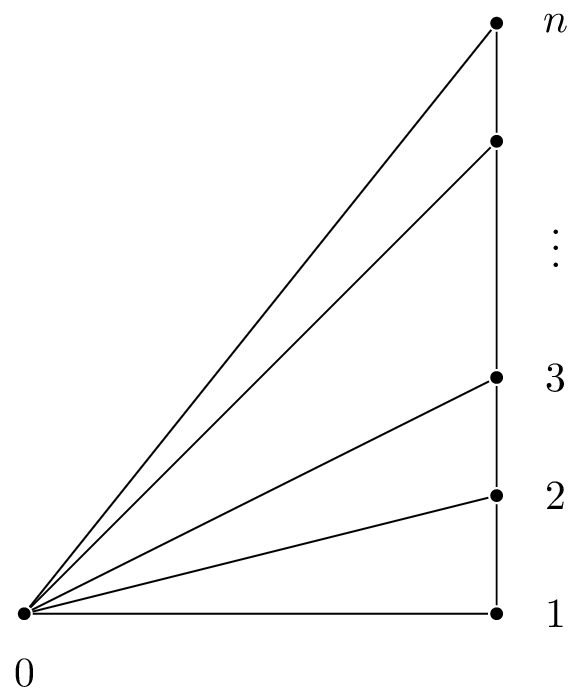
扇形图是指的如 Figure 1 所示之图。设 \(f_n\) 为有 \(n+1\) 个顶点的扇形图的生成树个数。直接计算可以知道 \(f_1=1\)、\(f_2=3\)、\(f_3=8\)。我们现在使用生成函数来计算其通项公式 \(f_n\)。

我们首先来推导 \(f_n\) 的递推式。考虑一个 \(n+1\) 顶点的扇形图中的生成树：

假设顶点 \(n\) 没有和顶点 \(0\) 连接，那么它一定和顶点 \(n-1\) 连接。在这种情况下，我们总共有 \(f_{n-1}\) 种生成树。
假设顶点 \(n\) 和顶点 \(0\) 相连。令 \(k\) 为最小的顶点编号，使得 \((n,n-1), (n-1,n-2),\dots, (k+1,k)\) 这些边一直存在在生成树中（即 \(n\) 与 \(k\) 通过一条路径直接连接，但 \(k\) 和 \(k-1\) 断开了）。一旦固定了 \(k\)，那么我们有在由顶点 \(\set{0,1,2,\dots,k-1}\) 组成扇形图中有 \(f_{k-1}\) 种生成树的选择。一种特殊情况是当 \(k=1\) 的时候，这条 \(1\) 到 \(n\) 的路径和 \((0,n)\) 本身就构成了一个生成树。

基于以上讨论，我们可以得到递推式 \[ f_n = f_{n-1} + \sum_{k<n}f_k + \^1[n>0]. \]

对上式左右乘上 \(z^n\) 并对所有的 \(n\in\^Z\) 求和，可以得到 \[ \begin{align*} \sum_n f_n z^n &=\sum_n f_{n-1} z^n+ \sum_{n} \tp{\sum_{k<n} f_k} z^n+\sum_n \^1[n>0] z^n. \end{align*} \] 注意到 \[ \begin{align*} \sum_{n} \tp{\sum_{k<n} f_k} z^n=\sum_kf_k\sum_{n>k}z^{n}= \sum_kf_kz^k\sum_{j>0}z^j= \sum_kf_kz^k\cdot\frac{1}{1-z}. \end{align*} \] 我们可以得到 \[ F(z) = zF(z) + F(z)\cdot \frac{z}{1-z} + \frac{z}{1-z}. \] 因此 \(F(z) = \frac{z}{1-3z+z^2}\)。我们可以使用类似在求解斐波那契数列的通项中的用到的技巧求解 \([z^n] F(z)\)。

生成函数的乘法

如果把两个生成函数相乘，他们对应的系数是卷积。 \[ [z^n]F(z)G(z) = \sum_{k} f_k g_{n-k}. \]

我们考虑一个对组合数的推广，即求解把 \(k\) 个相同的球扔到 \(n\) 个不同的箱子中，并且要求每个箱子中的球不超过 \(t\) 个的方案数。这个数列的生成函数是 \[ \begin{align*} (1+z+z^2+...+z^t)^n& = \tp{\frac{1-z^{t+1}}{1-z}}^n = \frac{1}{(1-z)^n}\cdot \tp{1-z^{t+1}}^n. \end{align*} \]

因此，我们可以使用上面提到的乘法规则计算 \([z^k]\tp{\frac{1}{(1-z)^n} \cdot \tp{1-z^{t+1}}^n}\)。

我们可以把这个乘法的规则推广到 \(n\) 个函数相乘。给定 \(F^{(1)}, F^{(2)}, \dots, F^{(m)}\) 满足 \(F^{(i)} = \sum_n f_n^{(i)}z^n\)，我们可以计算所谓的 \(m\)-次卷积： \[ [z^n]\tp{F^{(1)} F^{(2)}\cdots F^{(m)}} = \sum_{i_1+i_2+...+i_m = n}\prod_{j=1}^mf_{i_j}^{(j)}. \]

我们可以使用这个公式给出扇形图上生成树个数的另外一种计算方法：我们可以首先确定顶点 \(\set{1,2,\dots,n}\) 的连接方案，它对应于把整数 \(n\) 拆成若干个正整数之和。然后对应于这种连接方案的生成树个数就是这些正整数之积。比如说，在 Figure 2 所示的连接方案对应的生成树有 \(3\times 2\times 2=12\) 个。

根据上面的讨论，我们有 \(f_n=\sum_{m>0} \sum_{i_1+i_2+\cdots+i_m=n,\ i_j>0}\ i_1i_2\cdots i_m\)。设 \(G(z)\defeq \sum_{n>0}nz^n = \frac{z}{(1-z)^2}\)，那么 \(f_n = [z^n]\sum_{m>0}G(z)^m\)。因此，\(f_n\) 的生成函数是 \[ \begin{align*} F(z)=\sum_{m>0}G(z)^m = \frac{G(z)}{1-G(z)} = \frac{z}{1-3z+z^2}. \end{align*} \]

奇分划与不同数分划

整数 \(n\) 的一个奇分划指的是把它写成若干个奇数之和（不考虑顺序）的方式。比如 \(6=1+5=3+3=1+1+1+3=1+1+1+1+1\) 总共有 \(4\) 种奇分划。整数 \(n\) 的一个不同数分划指的是把它写成若干个不同的数之和（不考虑顺序）的方式。比如 \(6=6=1+5=2+4=1+2+3\) 总共有 \(4\) 中不同数分划。

欧拉使用生成函数巧妙的证明了下面这一个结论。

Proposition 1 任何整数 \(n>0\) 的奇分划个数和不同数分划个数相等。

分别设 \(O(z)\) 和 \(D(z)\) 为 \(n\) 的奇分划个数与不同数分划个数的生成函数。要证明 Proposition 1，我们只需证明 \(O(z)\) 和 \(D(z)\) 相等。我们首先来计算 \(O(z)\)： \[ \begin{align*} O(z) &= (1+z+z^2+z^3+\cdots)(1+z^3+(z^3)^2+(z^3)^3+\cdots)(1+z^5+(z^5)^2+(z^5)^3+\cdots)\cdots \\ &=\frac{1}{1-z}\cdot\frac{1}{1-z^3}\cdot\frac{1}{1-z^5}\cdots\\ &=\prod_{\mbox{\scriptsize odd }k} \frac{1}{1-z^k}. \end{align*} \] 另一方面，我们有 \[ \begin{align*} D(z) &=(1+z)(1+z^2)(1+z^3)(1+z^4)\cdots\\ &=\frac{1-z^2}{1-z}\cdot \frac{1-z^4}{1-z^2}\cdot \frac{1-z^6}{1-z^3}\cdot\frac{1-z^{8}}{1-z^4}\cdots\\ &=\prod_{\mbox{\scriptsize odd }k} \frac{1}{1-z^k} =O(z). \end{align*} \]