第五讲:偏序集
偏序集
我们今天开始研究偏序集,这是一种非常常见的结构。
偏序集的定义
Definition 1 偏序集 \((P,\le)\) 指的是一个集合 \(P\) 和一个偏序 \(\le\) 组成的二元组。在这儿,我们说一个二元关系 \(\le \subseteq P\times P\) 是偏序当且仅当其满足下面三个性质:
- (自反性) \(\forall a\in P\), \(a\le q\);
- (反对称性) \(\forall a,b\in P\),如果 \(a\le b\) 并且 \(b\le a\),那么 \(a=b\)。
- (传递性) \(\forall a,b,c\in P\),如果 \(a\le b\) 并且 \(b\le c\),那么 \(a\le c\)。
我们平时所说的全序集是一种特殊的偏序集,它需要额外满足 \(P\) 中任意两个元素都是可比较的,即 \(\forall a,b\in P\),要么 \(a\le b\),要么 \(b\le a\)。
对于偏序集 \((P,\le)\),我们会用记号 \(a<b\) 表示 \(a\le b\) 但 \(a\ne b\)。
举例来说,给定一个集合 \(U\),我们用 \(2^U\) 表示 \(U\) 的所有子集的集合,\(\subseteq\) 表示子集的包含关系,那么\(\tp{2^U,\subseteq}\) 就是一个偏序集。
整数上的整除关系也是一个偏序。给定 \(a,b\in\^Z\),定义 \(a\le b\) 当且仅当 \(a | b\)。那么 \(\tp{\^Z, \le}\) 是一个偏序集。
Hasse 图
我们用 Hasse 图来直观的展示一个偏序集。对于 \(a,b\in P\),我们连一条从 \(a\) 到 \(b\) 的边当且仅当 \(a<b\) 并且不存在 \(c\) 满足 \(a<c<b\)。每一个有限的偏序集都可以用一个 Hasse 图来表示。偏序集 \((2^{[3]},\subseteq)\) 的 Hasse 图如下:
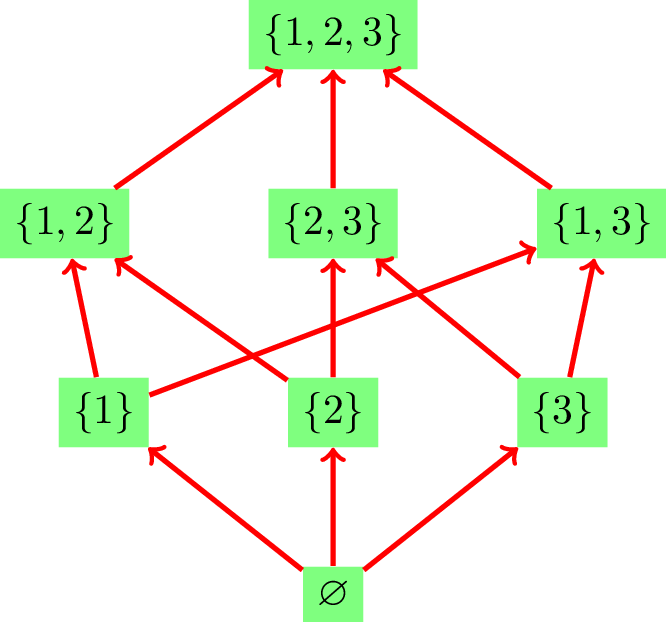
如果 \((P,\subseteq)\) 中元素 \(x\) 满足不存在任何 \(y\in P\) 使得 \(y>x\) 成立,则称 \(x\) 为一个极大(maximal)元素。如果 \(x\) 满足对于任何 \(z\in P\),都有 \(z\le x\),则称之为最大(maximum)元素。我们可以类似的定义极小元素和最小元素。显然,最大(最小)元素是极大(极小)元素,但反之则不一定。一个偏序集可能不存在最大和最小元素。同样,我们允许单独的顶点出现。
有单独元素出现的一个例子是 \(P=\set{2,3,4,5,6}\) 上的整除关系。 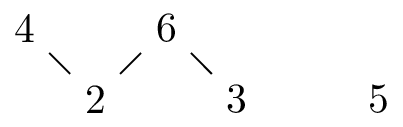
链与反链
在这一节,我们总是假定给定一个偏序集 \((P,\le)\)。
Definition 2 我们称一个集合 \(C\subseteq P\) 为链(chain),当且仅当 \[
\forall x,y\in C\colon x\le y \lor y\le x.
\]
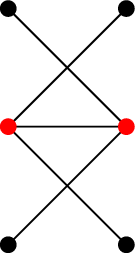
换句话说,一个链 \(C\) 中的任意两个元素在给定偏序的关系下是可比较的(但不一定在 Hasse 图中是连续的)。我们说一个链是极大的,当且仅当把任何一个其它的元素添加进去之后都不再是一个链。最大链则定义为元素最多的链。比如说,Figure 2 中, 绿色路径上的顶点形成了一条极大链,蓝色路径上的顶点形成了一条最大链。偏序集的高度(height)定义为最大链的大小。因此,Figure 2 中偏序集的高度为 \(5\)。
Definition 3 我们称一个集合 \(T\subseteq P\) 为反链(anti-chain),当且仅当 \[ \forall x,y\in T \colon x\ne y\implies x\not\le y \land y\not\le x. \]
也就是说,与链的概念对应,一个反链中的任意两个元素都是不可以比较的。我们可以类似的定义极大反链和最大反链。一个偏序集的宽度则被定义为其中最大反链的大小。Figure 2 中红色的顶点同时构成一个极大反链和最大反链。这个偏序集的宽度是 \(3\)。
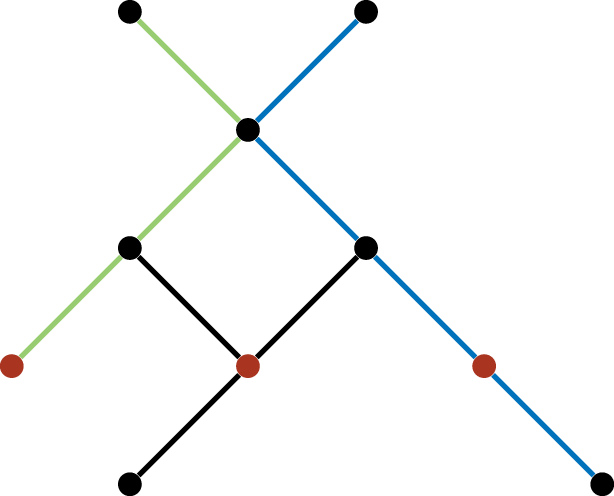
实际上,至少对于有限偏序集来说,子集的包含关系是一种最一般的偏序:我们可以从 Hasse 图中最下层的元素开始,对于每一个元素,把它定义成它自己与它在 Hasse 图中前继构成的集合。比如说,\(P=\set{2,3,4,5,6}\) 上的整除关系同构于 \(P'=\set{\set{2},\set{3},\set{5},\set{2,4},\set{2,3,6}}\) 上的子集包含关系。
链划分与反链划分
设 \((P,\le)\) 是一个偏序集。\(P\) 的一个链划分(Chain Partition)指的是一些不相交的链的集合 \(\+C=\set{C_1,C_2,\dots,C_m}\) 满足它们的并集正好是 \(P\),即 \(\bigcup \+C = P\) 且对任意 \(i,j\in [m]\),\(i\ne j\implies C_i\cap C_j=\emptyset\)。我们可以类似的定义反链划分(Anti-Chain Partition)为不相交的反链集合 \(\+A=\set{A_1,\dots,A_m}\),满足 \(\bigcup \+A = P\)。
接下来,我们将给出关于链划分与反链划分大小的的两个对偶定理。
Theorem 1 任何偏序集最小反链划分的大小等于其高度。
Proof. 设 \(r\) 为偏序集的高度。显然我们至少需要 \(r\) 个反链才能覆盖 \(P\)。因此,我们只需要构造一个包含恰好 \(r\) 个反链的划分。
我们对 \(r\) 进行归纳。在 \(r=1\) 的时候命题是显然成立的。假设 \(r>1\),首先我们从大小为 \(r\) 的每个链中取出最大的元素,这些元素一定构成组成一个反链。删除这些元素,然后在剩余高度为 \(r-1\) 的偏序集中使用归纳假设。我们便可以用 \(r\) 个不相交的反链覆盖原偏序集。
Theorem 2 (Dilworth 定理) 任何偏序集最小链划分的大小等于其宽度。
Proof. 设 \(w\) 是偏序集的宽度。显然至少需要 \(w\) 个链才能覆盖 \(P\)。我们只需要通过归纳证明 \(w\) 个链足以覆盖偏序集。
当 \(|P|=1\) 或 \(|P|=2\) 时,结论显然成立。设 \(C\subseteq P\) 是 \(P\) 中的最大链,令 \(P' = P\setminus C\)。
如果 \(P'\) 的宽度降到了 \(w-1\),那么由归纳假设,\(P'\) 可以被 \(w-1\) 条链覆盖。这种情况的证明就完成了。
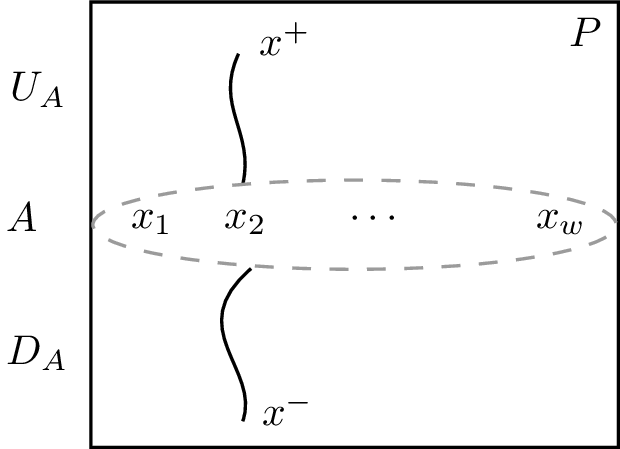
如果 \(P'\) 的宽度仍然是 \(w\),则令 \(P''=P\setminus\set{x^+,x^-}\),其中 \(x^+\) 和 \(x^-\) 分别是 \(C\) 中的最大和最小元素。那么 \(P''\) 中存在一个反链 \(A=\set{x_1,x_2,\dots,x_w}\),它把 \(P\) 分成了三个部分 \(A\sqcup U_A\sqcup D_A\),其中 \(U_A\triangleq\set{y\in P\mid\exists x\in A,x<y}\),\(D_A\triangleq\set{y\in P\mid \exists x\in A,y<x}\)。
注意到 \(x^+\) 必须在 \(U_A\) 中,\(x^-\) 必须在 \(D_A\) 中。因此我们有 \(\big|U_A\cup A \big|<|P|\) 和 \(\big|D_A\cup A \big|<|P|\) 成立。在 \(U_A\cup A\) 中应用归纳假设,我们可以找到 \(w\) 条不相交的链 \(C_{u_1},C_{u_2},\dots,C_{u_w}\),它们覆盖了 \(U_A\cup A\),其中 \(C_{u_i}\) 是包含 \(x_i\) 的链。同样地,我们有 \(D_A\cup A=C_{d_1}\sqcup C_{d_2}\sqcup \cdots\sqcup C_{d_w}\)。然后我们可以通过连接每个 \(C_{u_i}\) 和 \(C_{d_i}\) 来得到 \(P\) 中的 \(w\) 条更长的链。
\(A\sqcup B\) 表示非交并,即当我们写出这个记号的时候,默认了 \(A\cap B=\emptyset\)。
Min-Max 定理
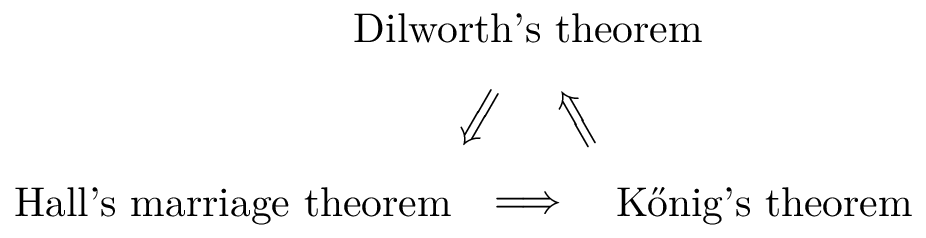
在组合数学、最优化等等很多数学领域会出现所谓的 Min-Max 类型的和 Dilworth 定理类似风味的结论。它们往往是某种对偶定理的具体表现形式。这一节,我们将介绍Hall 婚姻定理和Kőnig 定理,并且证明它们均和 Dilworth 定理等价。
\(N(S)\triangleq\set{y\in R \mid \exists x\in S, (x,y)\in E}\) 是 \(S\) 的邻居集合。
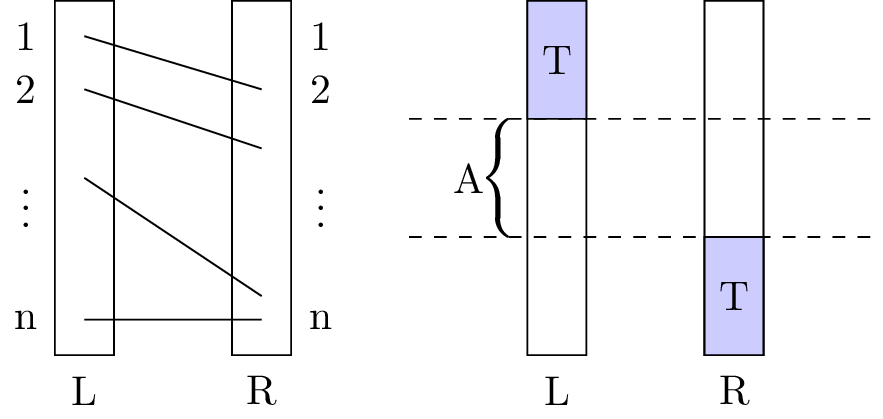
Theorem 3 (Hall 婚姻定理) 设 \(G=(L,R,E)\) 是一个二分图,其中 \(|L|=|R|=n\)。则 \(G\) 存在完美匹配当且仅当对于 \(L\) 的任意子集 \(S\),都有 \(\left|N(S)\right| \geq |S|\)成立。
我们使用 Dilworth 定理来证明 Hall 婚姻定理。
Proof. 必要性是显然的。我们来证明充分性,即当对于 \(L\) 的任意子集 \(S\),都有 \(\left|N(S)\right| \geq |S|\)成立时,\(G\) 存在完美匹配。设 \(P=L\cup R\)。构造如下偏序关系:若 \((l_i,r_j)\in E\),则 \(l_i\leq r_j\)。则 \(G\) 是 \(\tp{P,\leq}\) 的 Hasse 图。
我们现在来说明\(\set{r_1,r_2,\dots,r_n}\) 一定是最大反链(之一)。假设一个最大反链为 \(L_1\cup R_2\),其中 \(L_1\subseteq L\),\(R_2\subseteq R\),且 \(|L_1|+|R_2|>n\)。由 Hall 婚姻定理的条件,我们可以用 \(N(L_1)\) 代替 \(L_1\) 以得到另一个反链,其大小不小于 \(L_1\cup R_2\)。这与 \(\abs{R}=n\) 矛盾。因此,\((P,\leq)\) 的宽度为 \(n\)。根据Dilworth定理,存在\(n\)个不交的链覆盖 \(P\)。这 \(n\) 条链正好构成 \(G\) 的完美匹配。
我们可以用类似的方法说明,当 \(\abs{R}>\abs{L}=n\) 时,Hall 定理的条件可以保证一定存在大小为 \(n\) 的匹配。
点覆盖(Vertex Cover)是指包含每条边至少一个端点的顶点集合。
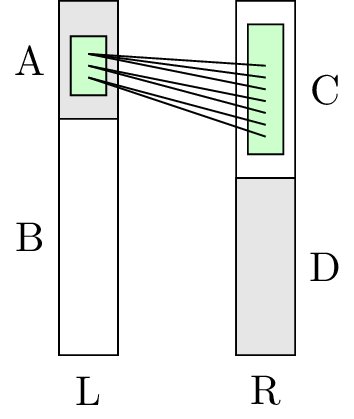
Theorem 4 在二分图 \(G=(L,R,E)\) 中,最大匹配的大小等于最小点覆盖的大小。
在上图中,最大匹配的大小 \(=\) 最小点覆盖(红色顶点)的大小 \(=2\)。
我们接下来使用 Hall 婚姻定理证明 Kőnig 定理。
Proof. 容易知道,一个顶点覆盖的大小始终不小于任何匹配的大小(因为对于任意一个匹配,顶点覆盖必须包含匹配的每条边上的至少一个顶点)。接下来我们证明:存在一个匹配,其大小与最小顶点覆盖的大小相同。
假设 \(A\cup D\) 是一个最小的顶点覆盖,其中 \(A\subseteq L\),\(D\subseteq R\)。那么根据上面的证明,对于任意的 \(S\subseteq A\),\(\abs{N(S)\cap C}\geq \abs{S}\)。也就是说,在子图\(G[A\cup C]\)中,\(A\) 满足 Hall 婚姻定理条件。否则,我们可以用更小的邻居集替换 \(A\) 中的某些 \(S\),得到一个更小的顶点覆盖。因此,\(G[A\cup C]\)中存在一个大小为\(|A|\)的匹配。类似地,我们可以在\(G[B\cup D]\)中找到一个大小为\(|D|\)的匹配。这形成了一个与最小顶点覆盖大小相同的匹配。
接下来,我们使用 Kőnig 定理证明 Dilworth 定理。
Proof.
设 \(V=\set{1,2,\dots,n}\),\(\leq\) 是 \(V\) 上的一个偏序。我们构造一个二分图 \(G=(L,R,E)\),其中 \(L=R=V\),\((i,j)\in E\) 当且仅当 \(i\leq j\)。
注意到,\(G\) 中的一个匹配 \(M\) 可以定义出一个不交的链覆盖:\(P=\set{C_1,C_2,\dots,C_m}\),其中 \(C_k=\set{x_1^{(k)}, x_2^{(k)},\dots,x_{n_k}^{(k)}}\) 满足 \(\tp{x_i^{(k)},x_{i+1}^{(k)}}\in M\)。每个 \(C_k\) 包含 \(M\) 中的 \(n_k-1\) 条边。因此,\(\sum_{k=1}^m (n_k-1)=\abs{M}\)。由于 \(\sum_{k=1}^m n_k =n\),所以有 \(n-m=\abs{M}\)。
此外,我们可以基于 \(G\) 中的一个顶点覆盖 \(S\) (可以看成顶点序号的一个“多重集”) 构造出 \(V\) 中的反链。令 \(T\) 为 \(S\) 中顶点序号构成的集合,即从多重集 \(S\) 中去掉重复元素后得到的集合(例如,如果 \(S=\set{1,1,2,3}\),则 \(T=\set{1,2,3}\)。)。令 \(A=V\setminus T\),则 \(A\) 是 \(\tp{V,\leq}\) 的一个反链。
根据 Kőnig 定理,如果我们选择最大匹配 \(M^*\) 和最小顶点覆盖 \(S^*\),则 \(\abs{M^*}=\abs{S^*}\)。那么 \[ \abs{A}=n-\abs{T}\geq n-\abs{S^*}=n-\abs{M^*}. \] 由于 \(n-\abs{M^*}=m\),我们有 \(\abs{A}\geq m\)。也就是说,我们可以用不超过 \(\abs{A}\) 条链覆盖偏序,其中 \(\abs{A}\) 不大于 \(\tp{V,\leq}\) 的宽度。
因此我们证明了,Hall 婚姻定理、Dilworth 定理和 Kőnig 定理是等价的。
Sperner 定理
在上一讲中我们已经展示了集合包含是一个规范偏序(至少对于有限偏序)。考虑一个典型的偏序 \(\tp{{2}^{[n]},\subseteq}\)。这个偏序的宽度(或者等价地,最大反链的大小)是多少呢?
Theorem 5 (Sperner 定理) \(\tp{{2}^{[n]},\subseteq }\) 的最大反链的大小为 \(\binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }\)。
Proof. 假设 \(\set{S_{1}, S_{2}, \cdots S_{w}}\) 是 \(\tp{{2}^{[n]},\subseteq }\) 的最大反链。注意到集合族 \(\binom{[n]}{\left \lfloor \frac{n}{2} \right \rfloor }\) 也是一个反链。因此,\(w\geq \binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }\)。我们只需要证明 \(w\leq \binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }\)。
对于任意 \(i\in[w]\),令 \({C}_{i}\) 是包含 \(S_{i}\) 的极大链的集合(换句话说,\({C}_{i}\) 中的每个元素都是从 \(\emptyset\) 到 \([n]\) 的 Hasse 图上经过 \(S_i\) 的一条路径)。因为从 \([n]\) 到 \(S_i\) 有 \((n-\abs{S_i})!\) 条路径,从 \(S_i\) 到 \(\emptyset\) 有 \(\abs{S_i}!\) 条路径,所以我们有 \(\abs{C_i}=(n-\abs{S_i})!\cdot \abs{S_i}!\)。
由于对于任意 \(i\neq j\) 且 \(i,j\in[w]\),都有 \(C_{i}\cap {C}_{j} = \emptyset\),我们有: \[ n!\ge \sum_{i=1}^{w} \left | {C}_{i} \right | = \sum_{i=1}^{w}(n-\left | S_{i} \right | )!\left | S_{i} \right |! = n!\sum_{i=1}^{w } \frac{(n-\left | S_{i} \right | )!\left | S_{i} \right |!}{n!} = n!\sum_{i=1}^{w } \binom{n}{\left | S_{i} \right | }^{-1}. \]
注意到对于任意 \(S_i\subseteq [n]\),都有 \(\binom{n}{\left | S_{i} \right | }\leq \binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }\)。因此, \[ 1\ge \sum_{i=1}^{w } \binom{n}{\left | S_{i} \right | }^{-1}\ge w\cdot\binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }^{-1}。 \] 这便可以推出 \(w\leq \binom{n}{\left \lfloor \frac{n}{2} \right \rfloor}\)。
Sperner 定理可以用来证明组合数学中的一些有趣结果。让我们来看一个例子。
Theorem 6 (Erdős, 1945) 假设\(x_{1}\),\(x_{2}\),\(\cdots\),\(x_{n}\)是\(n\)个实数,满足对于每个\(i\in [n]\),\(\left | x_{i} \right | \ge 1\)。令\(\eps=\tp{\eps_1,\eps_2,\cdots,\eps_n}\),其中每个 \(\eps_i\in\set{-1,1}\)。 则对于长度为 \(2\) 的开区间 \(I\),最多有 \(\binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }\) 个 \(\eps\) 满足 \(\sum_{i=1}^{n} \eps_{i}x_{i}\in I\)。
Proof. 不失一般性地假设每个\(x_i\geq 0\)。我们可以将每个 \(\eps\) 与唯一的集合 \(A=\set{i\in[n]\mid \eps_i=1}\) 相对应。令 \(S(A)\triangleq\sum_{i\in A}x_i-\sum_{j\notin A}x_j=\sum_{i=1}^{n} \eps_{i}x_{i}\)。然后对于任意的 \(A\subsetneq B\subseteq[n]\),\(\abs{S(A)-S(B)}\geq 2\)。
如果两个集合 \(A\) 和 \(B\) 满足 \(S(A)\in\tp{y,y+2}\) 和 \(S(B)\in\tp{y,y+2}\) 对于固定实数 \(y\) 同时成立,则有 \(\abs{S(A)-S(B)}< 2\)。因此,它们既不满足\(A\subsetneq B\),也不满足\(B\subsetneq A\)。这表明,在\(\set{A\subseteq[n]\mid S(A)\in I}\)中的集合彼此之间必须没有包含关系,并且形成\(\tp{2^{[n]},\subseteq}\)的一个反链。因此,根据 Sperner 定理,满足\(\sum_{i=1}^{n} \eps_{i}x_{i}\in I\) 的这样的 \(\eps\) 的数量不超过 \(\binom{n}{\left \lfloor \frac{n}{2} \right \rfloor }\)。