Lecture 12: Chaining, Dudley’s theorem
Recall that in the previous lecture, we derived a bound on the supremum of sub-Gaussian random variables with a Lipschitz condition.
Lemma 1 Suppose the \(\{X_t\}_{t\in T}\) are \(C\)-Lipschitz and that for every fixed \(t \in T\), the variable \(X_t\) is \(\sigma^2\)-sub-Gaussian. Then \[ \E{\sup_{t\in T} X_t}\leq \inf_{\eps>0} \tp{\eps \E{C} + \sqrt{2\sigma^2\cdot \log N(T,d,\eps)}}. \]
Here, \(N(T,d,\eps)\) is the covering number of the metric space \((T,d)\).
However, the condition that the process is \(C\)-Lipschitz (with a random variable \(C\) having finite expectation) is strong. For many interesting processes, such a \(C\) may not exist. In this lecture, we address cases where this condition is not satisfied. Most expositions follow (Vershynin 2018) and (Van Handel 2014).
The Dudley’s bound
We first introduce the sub-Gaussian process.
Definition 1 (Sub-Gaussian process) A stochastic process \(\{X_t\}_{t\in T}\) is called a \(\sigma^2\)-sub-Gaussian process with respect to a metric \(d\) if for any \(s,t\in T\), the increment \(X_t-X_s\) is a \(\sigma^2 \cdot d(s,t)^2\)-sub-Gaussian random variable.
For convenience, we assume \(\E{X_t}=0\) for each \(t\in T\). Our goal is to bound \(\E{\sup_{t\in T} X_t}\) for such a process. We cannot use the result from the previous lecture directly because finding a random variable \(C\) such that \(|X_t - X_s| \leq C \cdot d(s,t)\) almost surely is often impossible, or \(\E{C}\) would be infinite.
However, we can still adopt the key idea in the previous lecture. Let \(\mathcal{N}\) be an \(\varepsilon\)-net of \((T,d)\), and let \(\pi(t)\) denote the projection of \(t\) onto the closest point in \(\mathcal{N}\). We can decompose the process as \[ \sup_{t\in T} X_t \leq \sup_{t\in T} X_{\pi(t)} + \sup_{t\in T}\tp{X_t-X_{\pi(t)}}. \]
The first term is a supremum over the finite set \(\mathcal{N}\), which we know how to handle. The problem is the second term, \(\sup_{t\in T}(X_t - X_{\pi(t)})\), representing the fluctuations at scale \(\varepsilon\). Since we cannot use a Lipschitz property, we must treat it as another supremum problem.
This suggests a recursive approach. We can approximate the residual term using a finer \(\frac{\varepsilon}{2}\)-net, denoted by \(\mathcal{N}'\), with projection map \(\pi'\). The decomposition continues:
\[ \begin{align*} \sup_{t\in T} X_t &\leq \sup_{t\in T} X_{\pi(t)} + \sup_{t\in T}\tp{X_t-X_{\pi(t)}}\\ &= \sup_{t\in \+N} X_{\pi(t)} + \sup_{t\in T}\tp{X_t - X_{\pi'(t)} + X_{\pi'(t)} -X_{\pi(t)}}\\ &\leq \underbrace{\sup_{t\in T} X_{\pi(t)}}_{(A)} + \underbrace{\sup_{t\in T}\tp{X_{\pi'(t)} -X_{\pi(t)}}}_{(B)} + \underbrace{\sup_{t\in T}\tp{X_t - X_{\pi'(t)} }}_{(C)}. \end{align*} \]
Term \((A)\) is the supremum over the initial coarse net. Term \((B)\) is the supremum of increments between points in the finer net \(\mathcal{N}'\) and their predecessors in the coarser net \(\mathcal{N}\). Notably, the number of such pairs is finite. Term \((C)\) is the new residual term at the finer scale \(\varepsilon/2\).
We can deal with term \((C)\) inductively, repeating this decomposition at increasingly fine scales. This chaining technique gives Dudley’s theorem.
Theorem 1 (Dudley’s theorem (the summation version)) Assume \(\set{X_t}_{t\in T}\) is a \(\sigma^2\)-sub-Gaussian process on a metric space \((T,d)\). Then \[ \E{\sup_{t\in T} X_t} \leq 6\sigma\cdot \sum_{k\in \bb Z} 2^{-k}\cdot \sqrt{\log N(T,d,2^{-k})}. \]
Proof. We first consider the case where \(\abs{T}<\infty\).
Let \(k_0\) be the largest integer such that \(2^{-k_0}\geq \!{diam}(T)\) (\(k_0\) can be negative). Let \(\+N_k\) be a minimal \(2^{-k}\)-net ,so \(|\mathcal{N}_k| = N(T, d, 2^{-k})\). Let \(\pi_k(t)\) denote the projection of \(t\) in \(\mathcal{N}_k\). At the coarsest scale \(k_0\), \(\mathcal{N}_{k_0}\) can consist of a single arbitrary point, say \(t_0 \in T\), since every point in \(T\) is within distance \(\!{diam}(T)\) of \(t_0\). From the chainning argument, \[ \begin{align*} \E{\sup_{t\in T} X_t} &\leq \E{\sup_{t\in T} X_{\pi_{k_0}(t)}} + \E{\sup_{t\in T}\tp{X_t-X_{\pi_{k_0}(t)}}}\\ &= \E{\sup_{t\in T} X_{\pi_{k_0}(t)}} + \E{\sup_{t\in T}\tp{X_t - X_{\pi_{k_0+1}(t)} + X_{\pi_{k_0+1}(t)} -X_{\pi_{k_0}(t)}}}\\ &\leq \E{\sup_{t\in T} X_{\pi_{k_0}(t)}} + \E{\sup_{t\in T}\tp{X_{\pi_{k_0+1}(t)} -X_{\pi_{k_0}(t)}}} + \E{\sup_{t\in T}\tp{X_t - X_{\pi_{k_0}(t)} }}\\ &\leq \cdots\\ &\leq \E{X_{t_0}} + \sum_{k=k_0+1}^n \E{\sup_{t\in T}\tp{X_{\pi_{k}(t)} -X_{\pi_{k-1}(t)}}} + \E{\sup_{t\in T}\tp{X_t -X_{\pi_{n}(t)}}}. \end{align*} \] By assumption, the process is centered, so \(\E{X_{t_0}}=0\). We can choose a large enough \(n\) such that \(\+N_n=T\) and \(\E{\sup_{t\in T}\tp{X_t -X_{\pi_{n}(t)}}}=0\).
By the definition of \(\eps\)-nets, for any \(t\in T\), \[
d\tp{\pi_k(t), \pi_{k-1}(t)}\leq d\tp{\pi_k(t), t} + d\tp{t, \pi_{k-1}(t)} \leq 3\cdot 2^{-k}.
\]
The increment \(X_{\pi_k(t)} - X_{\pi_{k-1}(t)}\) is therefore \(\sigma^2\cdot \tp{3\cdot 2^{-k}}^2\)-sub-Gaussian. The supremum \(\sup_{t\in T} (X_{\pi_k(t)} - X_{\pi_{k-1}(t)})\) is taken over a finite set of random variables. Specifically, the cardinality of this set is bounded by \(|\mathcal{N}_k| \cdot |\mathcal{N}_{k-1}| \leq |\mathcal{N}_k|^2\). Using the maximal inequality for sub-Gaussian variables from the previous lecture, we have \[
\E{\sup_{t\in T}\tp{X_{\pi_{k}(t)} -X_{\pi_{k-1}(t)}}} \leq 6\cdot 2^{-k}\sigma\sqrt{\log \abs{\+N_k}}
\] and consequently, \[
\E{\sup_{t\in T} X_t}\leq 6\sigma \sum_{k=k_0+1}^n 2^{-k}\sqrt{\log \abs{\+N_k}} \leq 6\sigma\cdot \sum_{k\in \bb Z} 2^{-k}\cdot \sqrt{\log N(T,d,2^{-k})}.
\]
If \(T\) is infinite and separable, the result follows by taking a limit over an increasing sequence of finite subsets that are dense in \(T\).
Corollary 1 (Dudley’s theorem (the integral version)) Assume \(\set{X_t}_{t\in T}\) is a \(\sigma^2\)-sub-Gaussian process. We have \[ \E{\sup_{t\in T} X_t} \leq 12\sigma\cdot \int_0^{\infty} \sqrt{\log N(T,d,\eps)}\ \dd \eps. \]
Proof. From the summation version of Dudley’s theorem, \[ \E{\sup_{t\in T} X_t} \leq 6\sigma\cdot \sum_{k\in \bb Z} 2^{-k}\cdot \sqrt{\log N(T,d,2^{-k})}. \] We can interpret the sum as a Riemann sum approximation of the integral. That is, \[ \begin{align*} \sum_{k\in \bb Z} 2^{-k}\cdot \sqrt{\log N(T,d,2^{-k})} &= 2 \sum_{k\in \bb Z} \int_{2^{-k-1}}^{2^{-k}} \sqrt{\log N(T,d,2^{-k})}\ \dd \eps\\ &\leq 2 \sum_{k\in \bb Z} \int_{2^{-k-1}}^{2^{-k}} \sqrt{\log N(T,d,\eps)}\ \dd \eps\\ &= 2\int_0^{\infty} \sqrt{\log N(T,d,\eps)}\ \dd \eps \end{align*} \]
Dudley’s theorem is a powerful tool for bounding the suprema of various random variables. We now turn to some concrete applications.
The Monte Carlo method
Consider a random variable \(X\) distributed according to a measure \(\mu\) (e.g., the Lebesgue measure on \([0,1]\)), and a function \(f: \mathbb{R} \to \mathbb{R}\). We can estimate the expectation \(\E{f(X)}\) by sampling \(n\) independent points \(X_1, \dots, X_n \sim \mu\) and computing the empirical average:\[\frac{1}{n}\sum_{i=1}^n f(X_i).\] By the law of large numbers, this approximation converges to \(\E{f(X)}\).
The error of this estimator is standard to analyze: \[ \begin{align*} \E{\abs{\frac{1}{n} \sum_{i=1}^n f(X_i) - \E{f(X)}}} &\leq \E{\tp{\frac{1}{n} \sum_{i=1}^n f(X_i) - \E{f(X)}}^2}^{\frac{1}{2}}\\ &=\sqrt{\frac{\Var{f(X_1)}}{n}}. \end{align*} \]
Now, suppose we have a family of functions \(\+F=\set{f_1,f_2\dots}\). We want to approximate the expectations of all these functions simultaneously using the same set of \(n\) samples. Can we guarantee that the maximum error over the entire class is small? In other words, we want to bound \[ \sup_{f \in \mathcal{F}} \left| \frac{1}{n} \sum_{i=1}^n f(X_i) - \E{f(X)} \right|. \] If \(\mathcal{F}\) is finite, a union bound suggests the error grows as \(\frac{|\mathcal{F}|}{\sqrt{n}}\), which fails if \(|\mathcal{F}|\) is large or infinite. However, if the functions in \(\mathcal{F}\) are structurally related (e.g., they are all Lipschitz), the “effective” size of \(\mathcal{F}\) is much smaller.
In this section, we show that when the functions in \(\+F\) are Lipschitz, the total error can be bounded. We prove the following theorem.
Theorem 2 (Law of large numbers for Lipschitz functions) Let \[ \+F=\set{f:[0,1]\to [0,1], f \mbox{ is }1\mbox{-Lipschitz}}. \] Let \(X_1,\dots,X_n\) be \(n\) independent samples uniformly drawn from \([0,1]\). Define \(X_f=\frac{1}{n} \sum_{i=1}^n f(X_i)-\E{f(X)}\) for any \(f\in \+F\). Then the expected error satisfies \[ \E{\sup_{f\in \+F} X_f} = \+O\tp{\frac{1}{\sqrt{n}}}. \]
We will apply Dudley’s theorem to prove this. For any two functions \(f, g \in \mathcal{F}\), define the random variable \[ Z_i= (f-g) (X_i) - \E{f-g} \] It is easy to check that \(Z_i\) is \(\norm{f-g}^2_{\infty}\)-sub-Gaussian. By the additivity of sub-Gaussian variance, \[ X_f-X_g = \frac{1}{n} \tp{\sum_{i=1}^n (f-g) (X_i) - \E{f-g}}. \] is \(\frac{\norm{f-g}^2_{\infty}}{n}\)-sub-Gaussian. Thus, \(\{X_f\}\) is a \(1/n\)-sub-Gaussian process. Dudley’s theorem gives us \[ \E{\sup_{f\in \+F} X_f} \leq \frac{12}{\sqrt{n}} \int_0^{1} \sqrt{\log \+N\tp{\+F, \norm{\cdot}_{\infty}, \eps}}\ \dd \eps. \]
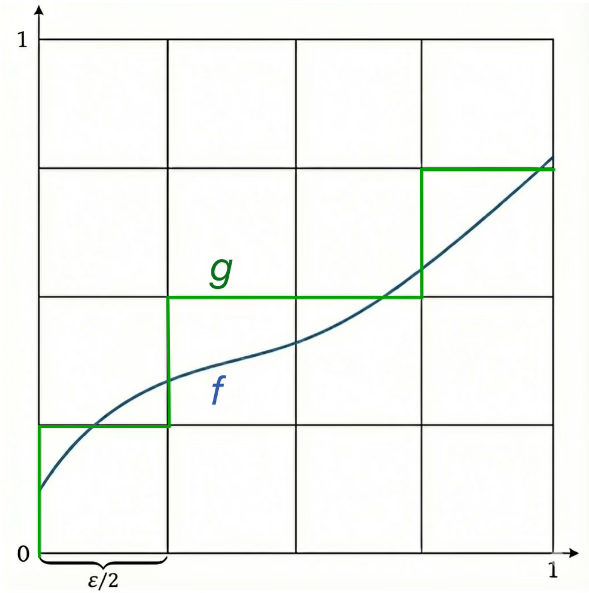
Now it remains to calculate the covering number \(\+N\tp{\+F, \norm{\cdot}_{\infty}, \eps}\). We discretize the domain \([0,1] \times [0,1]\) into a grid of scale \(\varepsilon/2\). As shown in the figure, any 1-Lipschitz function \(f\) (blue) can be approximated by a grid path \(g\) (green) within distance \(\varepsilon/2\).
The grid paths \(g\) themselves may not be 1-Lipschitz (e.g., they may be step functions) and thus might not belong to \(\mathcal{F}\). However, they form an “external” \(\varepsilon/2\)-net. For each grid path \(g\) close to some \(f \in \mathcal{F}\), we simply pick one valid representative \(f_g \in \mathcal{F}\) such that \(\|f_g - g\|_\infty \leq \varepsilon/2\). By the triangle inequality, for any \(f\) approximated by \(g\): \[ \|f - f_g\|_\infty \leq \|f - g\|_\infty + \|g - f_g\|_\infty \leq \varepsilon. \] Thus, the set of representatives \(\{f_g\}\) forms a valid \(\varepsilon\)-net for \(\mathcal{F}\).
The number of such grid paths is roughly bounded by counting the valid moves at each step. There are \(2/\varepsilon\) steps, and at each step, the function can go up, down, or stay flat (roughly constant choices). A combinatorial argument bounds the covering number by \[ \log N(\mathcal{F}, \|\cdot\|_{\infty}, \varepsilon) \approx O\left(\frac{1}{\varepsilon}\right). \]
Therefore, \[ \E{\sup_{f\in \+F} X_f} \lesssim \frac{1}{\sqrt{n}} \int_0^{1} \sqrt{\frac{1}{\eps}} \dd \eps = \+O\tp{\frac{1}{\sqrt{n}}}. \]
High-dimensional generalization
This grid argument generalizes to functions \(f: [0,1]^d \to [0,1]\). However, the complexity of the function class grows exponentially with dimension: \[ \log N(\mathcal{F}, \|\cdot\|_{\infty}, \varepsilon) \approx O\left(\varepsilon^{-d}\right). \] Substituting this into Dudley’s integral leads to a problem for \(d \geq 2\): \[ \int_0^1 \sqrt{\varepsilon^{-d}}\ \dd \varepsilon = \int_0^1 \varepsilon^{-d/2}\ \dd \varepsilon . \] This integral diverges near 0 for \(d \geq 2\) and it indicates the full chaining down to \(\varepsilon=0\) is too loose. We must stop the chaining at a small \(\delta > 0\) and handle the remainder separately. By slighly modifying the proof of Dudley’s theorem, we can get \[ \E{\sup_{f\in \+F} X_f} \lesssim \delta + \frac{1}{\sqrt{n}} \int_{\delta}^{1} \sqrt{\log \+N\tp{\+F, \norm{\cdot}_{\infty}, \eps}} \dd \eps,\quad \forall \delta\in [0,1]. \] Optimizing \(\delta\) yields the convergence rates:
When \(d=2\), we have \[ \E{\sup_{f\in \+F} X_f}\lesssim \delta + \frac{\log \delta^{-1}}{\sqrt{n}}. \] Choosing \(\delta = 1/\sqrt{n}\), we get a rate of \(\+O\tp{\frac{\log n}{\sqrt{n}}}\).
When \(d>2\), we have \[ \E{\sup_{f\in \+F} X_f}\lesssim \delta + \frac{\delta^{1-\frac{d}{2}}}{\sqrt{n}}. \] Choosing \(\delta = n^{-1/d}\), we get a rate of \(\+O\tp{n^{-\frac{1}{d}}}\).
The ellipsoid example
We now examine a case where Dudley’s theorem yields a suboptimal bound. This highlights that while chaining is powerful, it is not always the tightest method for every geometry.
Let \(g \in \mathbb{R}^n\) be a standard Gaussian vector, \(g_i \sim \mathcal{N}(0,1)\). We want to bound the supremum of the linear process indexed by an ellipsoid \(\mathcal{E}\). Define the ellipsoid with semi-axes \(1\geq \sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_n > 0\): \[ \mathcal{E} = \left\{ t \in \mathbb{R}^n : \sum_{i=1}^n \frac{t_i^2}{\sigma_i^2} \leq 1 \right\}. \]
Recall that a similar but simpler problem has been discussed when we bounded the norm of a random matrix in previous lectures. We considered the case where \(\+E\) degenerates to the ball \(B_2^n\) and proved that the covering number \(N\tp{B_2^n, \norm{\cdot}, \eps} \approx \tp{\frac{1}{\eps}}^n\).
In this section, we are interested in \(Z = \sup_{t \in \mathcal{E}} \langle g, t \rangle\). Note that we can write \(\mathcal{E} = A B_2^n\), where \(A = \text{diag}(\sigma_1, \dots, \sigma_n)\). By a simple change of variables \(t = Ax\), we have \[ \begin{align*} \sup_{t\in \+E} \inner{g}{t} &= \sup_{x\in B_n} \inner{g}{Ax} = \sup_{x\in B_n} \inner{Ag}{x} = \norm{Ag}_{\!{op}} = \sqrt{\sum_{i=1}^n \sigma_i^2 g_i^2}. \end{align*} \]
The Dudley’s bound
To apply Dudley’s theorem, we need to bound the covering number \(N(\mathcal{E}, \|\cdot\|_2, \varepsilon)\). Geometrically, covering the ellipsoid \(\mathcal{E}\) with \(\varepsilon\)-balls is similar to covering the box defined by the axes. The “effective dimension” at scale \(\varepsilon\) is the number of axes larger than \(\varepsilon\): \[
d(\varepsilon) = \max \{ k : \sigma_k \geq \varepsilon \}.
\] As illustrated in the figure, for axes \(k \le d(\varepsilon)\), we need roughly \(\sigma_k / \varepsilon\) balls to cover that dimension. For axes \(k > d(\varepsilon)\), one ball suffices. Thus, \[
\log N(\mathcal{E}, \|\cdot\|_2, \varepsilon) \approx \sum_{k=1}^{d(\varepsilon)} \log \left( \frac{\sigma_k}{\varepsilon} \right) \lesssim d(\eps)\cdot \log\tp{\frac{1}{\eps}}.
\] 
It is obvious that this is a \(1\)-sub-Gaussian process. Substituting the above formula into Dudley’s bound yields: \[
\E{\sup_{t\in \+E} \inner{g}{t}} \lesssim \int_0^{\infty} \sqrt{d(\eps)\cdot \log\tp{\frac{1}{\eps}}}\ \dd \eps =\tilde{\+O}\tp{\sum_{k=1}^n \frac{\sigma_k}{\sqrt{k}}},
\] where logarithmic terms are omitted for simplicity.
The single-step bound
In this specific case, we can do better by not chaining all the way down. We still consider a minimal \(\eps\)-net of \(\+E\) and decompose the target in the same way: \[ \sup_{t \in \mathcal{E}} \langle g, t \rangle \leq \sup_{t \in \mathcal{E}} \langle g, t - \pi(t) \rangle + \sup_{t \in \mathcal{E}} \langle g, \pi(t) \rangle. \] The second term can be bounded using the size of the \(\eps\)-net: \[ \E{\sup_{t \in \mathcal{E}} \langle g, \pi(t) \rangle} \lesssim \sqrt{\log N(\mathcal{E}, \|\cdot\|_2, \varepsilon)} \lesssim \sqrt{d(\eps)\cdot \log\tp{\frac{1}{\eps}}}. \] For the first term, note that for those axes \(i>d(\eps)\), \(\abs{t_i-\pi(t)_i}\leq \sigma_i\), and for \(i\leq d(\eps)\), \(\abs{t_i-\pi(t)_i}\leq \eps\leq \sigma_{d(\eps)}\). Therefore, \[ \begin{align*} \E{\sup_{t \in \mathcal{E}} \langle g, t - \pi(t) \rangle} \leq \E{\sum_{i=1}^{d(\eps)}\sigma_{d(\eps)}\abs{g_i} + \sum_{i>d(\eps)} \sigma_{i}\abs{g_i}} \lesssim \sqrt{d(\eps)\cdot \sigma^2_{d(\eps)} + \sum_{i>d(\eps)} \sigma^2_i} \end{align*} \] Thus, this single-step decomposition gives a bound of \[ \E{\sup_{t\in \+E} \inner{g}{t}} \lesssim \inf_{\eps} \sqrt{d(\eps)\cdot \sigma^2_{d(\eps)} + \sum_{i>d(\eps)} \sigma^2_i} + \sqrt{d(\eps)\cdot \log\tp{\frac{1}{\eps}}}, \] which is better than Dudley’s bound in general.