第十三讲:乘积概率空间,富比尼-托内利定理
乘积测度空间
在我们上一周的作业里,我们让大家举反例说明如下命题是不对的:如果每一个 \(X_i\) 均可积,那么 \[ \E{\sum_{i=1}^\infty X_i} = \sum_{i=1}^\infty\E{X_i}. \] 我们知道,无论是期望还是求和,都可以看成在某个测度下的勒贝格积分。因此,我们今天想来回答,在什么条件下,积分是可以交换的,即 \[ \int_{A}\tp{\int_B f\d P}\d Q = \int_{B}\tp{\int_A f\d Q}\d P \] 成立。我们首先来定义乘积测度空间。
假设我们有两个概率空间 \((X,\@X,\mu)\) 和 \((Y,\@Y,\nu)\)。我们可以想象
- 第一个概率空间是掷一个骰子得到 \(\omega_1\in X\),第二个概率空间是掷另一个骰子,得到 \(\omega_2\in Y\);或者
- 第一个概率空间是在 \([0,1]\) 上均匀取一个数 \(a\),第二个概率空间是在 \([0,2]\) 上均匀取一个数 \(b\)。
我们现在可以考虑一个概率空间,称为乘积概率空间,他的样本集是 \(X\times Y\),用来表示独立的做两次实验。在我们上面的两个例子里,分别对应了:
- 同时投两枚骰子,得到 \((\omega_1,\omega_2)\);
- 在 \([0,1]\times [0,2]\) 上均匀取一个点 \((a,b)\)。
所以一个自然的问题是,这个乘积概率空间里,事件集和测度应该是什么。离散概率空间比较平凡,我们考虑上面第二个例子。这个时候 \(\@X=\@B([0,1])\),\(\@Y = \@B([0,2])\)。集合 \(\@X\times \@Y = \set{A\times B\cmid A\in \@X, B\in \@Y}\) 是 \([0,1]\times [0,2]\) 上所有“矩形”的集合。它显然不是一个 \(\sigma\)-代数,因此,我们可以取乘积概率空间的事件集为 \(\sigma(\@X\times \@Y)\),并把它记做 \(\@X\otimes \@Y\)。
更一般的,对于两个测度空间 \((X,\@X,\mu)\) 和 \((Y,\@Y,\nu)\),我们定义它的乘积空间为 \((X\times Y,\@X\otimes \@Y)\),其中 \(\@X\otimes\@Y \defeq \sigma(\@X\times \@Y)\)。我们接下来定义 \(\@X\otimes\@Y\) 上的测度。看起来有两种比较自然的定义方式。
给定一个集合 \(E\in \@X\otimes\@Y\),我们定义两个函数 \(E^1\colon x\in X\mapsto E^1(x)\subseteq Y\) 和 \(E^2\colon y\in Y\mapsto E^2(y)\subseteq X\),分别表示集合 \(E\) 在 \(X=x\) 和 \(Y=y\) 上的投影,如下图所示。 \[ \begin{align*} E^1(x)&\defeq \set{y\in Y\cmid (x,y)\in E}\\ E^2(y)&\defeq \set{x\in X\cmid (x,y)\in E}. \end{align*} \]
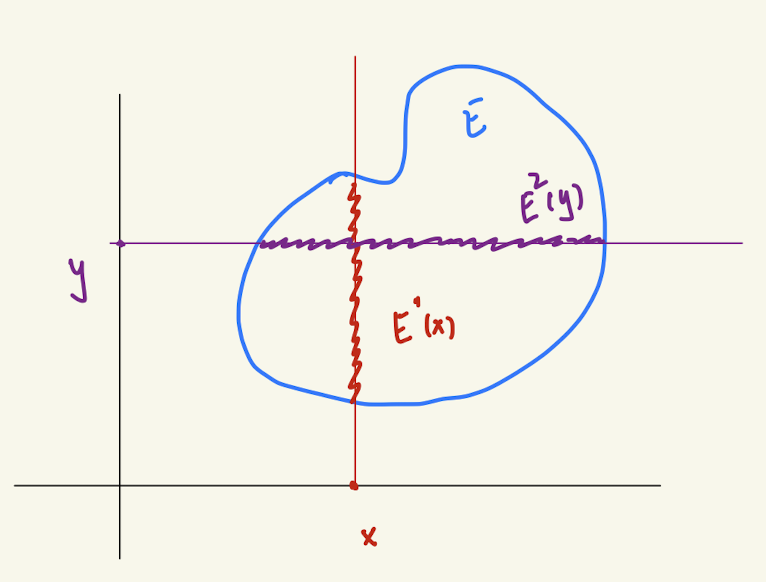
我们需要说明,如果 \(E\) 是 \(\@X\otimes\@Y\) 可测的,那么对于任意 \(x\) 和 \(y\),\(E^1(x)\) 与 \(E^2(y)\) 分别是 \(\@Y\) 与 \(\@X\) 可测的。
Proposition 1 如果 \(E\) 是 \(\@X\otimes\@Y\) 可测的,那么对于任意 \(x\) 和 \(y\),\(E^1(x)\) 与 \(E^2(y)\) 分别是 \(\@Y\) 与 \(\@X\) 可测的。
我们把命题的证明放到本次讲义的最后,先来继续我们的讨论。
于是,我们可以定义 \[ \begin{align*} \pi^1(E) &\defeq \int_X \nu(E^1(x))\mu(\dd x);\\ \pi^2(E) &\defeq \int_Y \mu(E^2(y))\nu(\dd y). \end{align*} \] 换句话说,\(\pi^1(E)\) 和 \(\pi^2(E)\) 分别对应着在计算 \(E\) 的面积的时候“横着积”和“竖着积”。设 \[ \@G =\set{E\in \@X\otimes\@Y\cmid \pi^1(E) = \pi^2(E)} \] 为所有 \(\pi^1(E)\) 和 \(\pi^2(E)\) 相等的可测集的集合。对于矩形 \(E=A\times B\in\@X\times \@Y\),我们显然有 \[ \pi^1(E) = \pi^2(E) = \mu(A)\times \mu(B), \] 即 \(\@X\times \@Y\subseteq \@G\)。如果 \(\mu\) 和 \(\nu\) 均是 \(\sigma\)-有限的,我们可以使用单调类定理说明 \(\@X\otimes\@Y\subseteq \@G\) (留作练习)。所以,我们可以定义测度 \[ \forall E\in\@X\otimes\@Y,\;\tp{\mu\otimes\nu}(E)\defeq \pi^1(E)=\pi^2(E). \] 于是,\((X\times Y,\@X\otimes\@Y,\mu\otimes\nu)\) 便是我们构造出来的乘积空间。
我们考虑一个特殊的例子。设 \(X=Y=\bb R\),\(\@X=\@Y = \@B(\bb R)\),\(\mu=\nu=\lambda\)。那么 \((X,\@X,\mu)\) 和 \((Y,\@Y,\nu)\) 均为一维的 \(\bb R\) 上的勒贝格测度空间。按照我们的定义,它的乘积空间是 \((\bb R^2,\@B(\bb R)^{\otimes 2},\lambda^{\otimes 2})\)。同样根据定义,我们知道 \(\@B(\bb R)^{\otimes 2}\) 就是 \(\@B(\bb R^2)\),并且根据 Carathéodory 定理,\(\lambda^{\otimes 2}\) 就是 \(\bb R^2\) 上的勒贝格测度。
我们的定义可以推广到任意有限个概率空间的乘积。对于无穷多个概率空间的乘积,情况比较复杂,超出了这门课的范畴,可以参见 Kolmogorov extension theorem。
富比尼-托内利定理(Fubini-Tonelli’s Theorem)
富比尼-托内利定理说的是,如果一个定义在乘积空间 \((X\times Y,\@X\otimes \@Y,\mu\otimes \nu)\) 上的可测函数 \(f\) 非负,或者可积,那么有等式 \[ \int_{X\times Y} f(x,y)\mu\otimes\nu(\dd x\dd y) = \int_X\tp{\int_Yf(x,y)\nu(\dd y)}\mu(\dd x) = \int_Y\tp{\int_X f(x,y) \mu(\dd x)}\nu(\dd y) \] 成立。也就是说,积分的顺序可以任意交换。当然,这个等式成立需要先保证对于任意 \(x\),函数 \(f(x,\cdot)\colon y\in Y\mapsto f(x,y)\in \bb R\) 是可测的 (对函数 \(f(\cdot,y)\) 同理)。这是上一节关于 \(E^1\) 和 \(E^2\) 函数可测的更一般版本。我们将在最后一节证明。
值得强调的是,关于 \(f\) 的可积性要求是 \(f\) 在\(\mu\otimes\nu\) 这个乘积测度上是可积的,如果仅仅是对于任何 \(x\in X\), \(f(x,\cdot)\) 在 \(\nu\) 上可积,或者对于任何 \(y\in Y\),\(f(\cdot,y)\) 在 \(\mu\) 上可积,是不够的。我们本次课一开始提到的的那个反例就说明了这一点。
我们简单叙述一下定理的证明,类似的套路大家现在应该很熟悉了,具体的细节请大家自己完成。我们只讨论 \(f\ge 0\) 的情况,\(f\) 可积的情形可以转化为分别考虑 \(f^+\) 与 \(f^-\) 两个非负函数。
- 首先,如果 \(f = \bb I_E\) ,其中 \(E\) 是某个可测集。那么此时,我们想要证明的等式即我们上一节验证过的“横着积”等于“竖着积”的测度等式。
- 然后,我们考虑 \(f\) 的下近似 \(\ul f_n\)。对于每一个 \(n\),它都可以写成 \(\sum_i c_i\cdot \bb I_{E_i}\) 的形式,其中 \(E_i\) 是可测集。于是,使用期望的线性性,我们可以证明此时的等式。
- 使用 MCT,我们可以对 \(\ul f_n\) 的积分求极限,得到对 \(f\) 的积分。
在具体使用 Fubini-Tonelli 的时候,我们往往是这样做的。
- 如果 \(f\) 非负,那么可以随意的交换积分顺序进行计算。
- 如果 \(f\) 可正可负,我们先对 \(\abs{f}\) 计算某一个累次积分,比如 \(\int_X \tp{\int_Y \abs{f}\d\nu}\d\mu\)。如果其 \(<\infty\),那么就说明它满足我们定理的条件。
\(f(x,\cdot)\),\(f(\cdot,y)\) 可测的证明
我们接下来证明在乘积测度空间 \((X\times Y,\@X\otimes \@Y,\mu\otimes\nu)\) 上的可测函数 \(f\colon (x,y)\in X\times Y\mapsto \bb R\) 的限制 \(f(x,\cdot)\colon y\in Y\mapsto f(x,y)\) 和 \(f(\cdot,y)\colon x\in X\mapsto f(x,y)\) 分别是在 \(\@Y\) 和 \(\@X\) 上可测的。
我们证明 \(f(x,\cdot)\) 的情况。考虑一个固定的 \(x\in X\) 以及一个函数 \[ T_x\colon y\in Y\mapsto (x,y)\in X\times Y. \] 显然,\(f(x,\cdot) = f\circ T_x\)。我们只需要验证 \(T_x\) 是从 \((X,\@X)\) 到 \((X\times Y,\@X\otimes\@Y)\) 的可测函数即可。因为容易验证,两个可测函数的复合函数还是一个可测函数。
为了验证 \(T_x\) 是一个可测函数,我们只需要验证,对于每一个 \(X\times Y\) 里的矩形 \(A\times B\),\(T_x^{-1}(A\times B)\in \@X\) 即可(我们以前证明过这件事情,还记得吗)。但 \[ T_x^{-1}(A\times B) = \begin{cases} B, & \mbox{ if $x\in A$;}\\ \emptyset, & \mbox{if $x\not\in A$.} \end{cases} \] 因此 \(T_x\) 是可测的。