第十七讲:一些经典概率问题
我们今天使用学过的工具来解决一些经典的概率问题。这一部分的内容主要来自 William Feller 的名著 An introduction to probability theory and its applications。
线段和圆环上的点
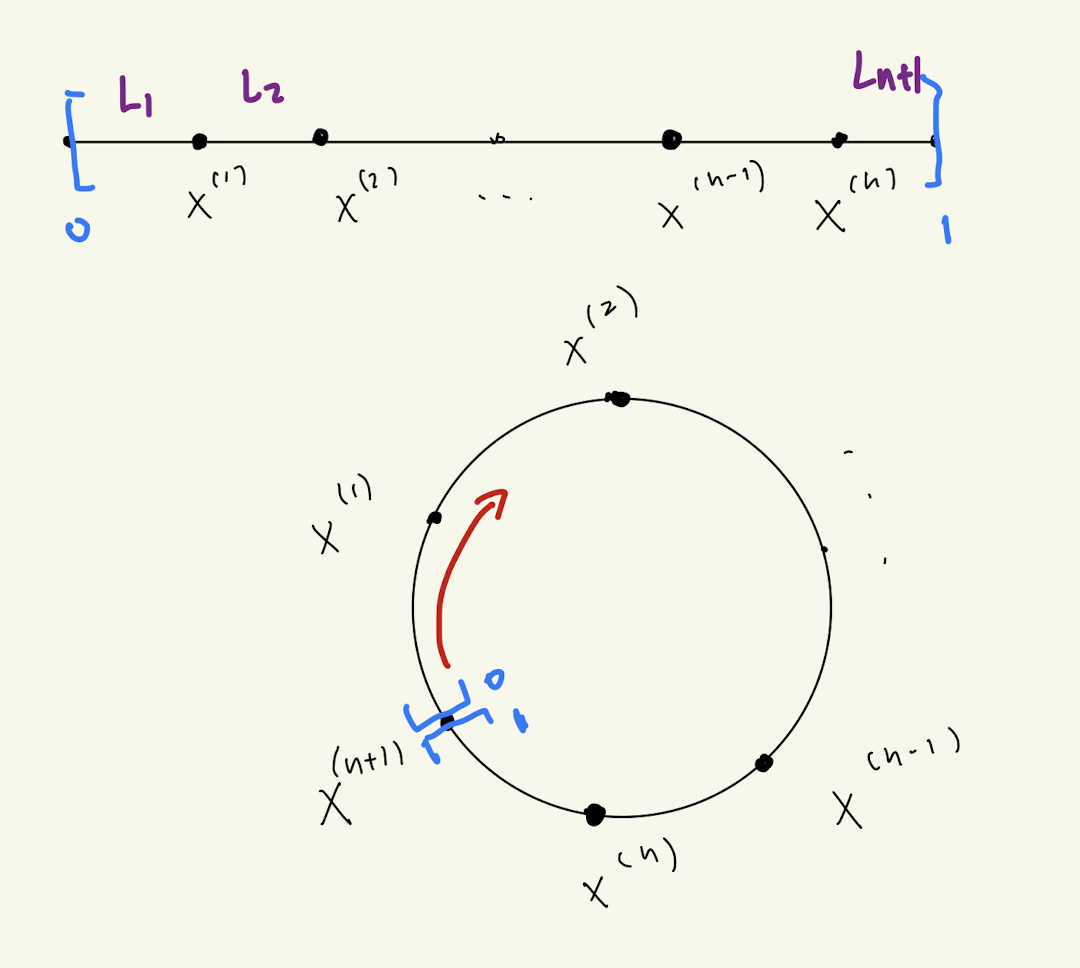
在 \([0,1]\) 线段上均匀的扔 \(n\) 个点 \(X_1,X_2,\dots,X_n\)。我们把它们从小到大排列后叫做 \(X^{(1)}\le X^{(2)}\le\cdots\le X^{(n)}\)。这 \(n\) 个点把 \([0,1]\) 分成了 \(n+1\) 个线段 \([0,X^{(1)}],[X^{(1)},X^{(2)}],\dots,[X^{(n-1)},X^{[n]}],[X^{[n]},1]\)。我们分别用 \(L_1,L_2,\dots,L_{n+1}\) 来表示这些线段长度。现在的问题是,对于 \(i\in[n+1]\),\(L_i\) 是同分布的吗?
它们确实是同分布的。我们可以做这样一个思想实验。假设我们在周长为 \(1\) 的圆周上均匀的扔 \(n+1\) 个点,这 \(n+1\) 个点把圆周分成了 \(n+1\) 段,根据对称性,这 \(n+1\) 段的长度一定是同分布的。我们随便选一个点,把它标记为原点,把圆周从这里断开成一个 \([0,1]\) 线段,从它开始按照顺时针经过的点叫做 \(X^{(1)}, X^{(2)},\dots, X^{(n)}\)。这样得到的 \(n\) 个点和我们在 \([0,1]\) 上均匀的扔 \(n\) 个点一定是同分布的,因此,他们划分的线段长度也是同分布的。
我们容易计算出 \(\Pr{L_1>t} = (1-t)^n\)。由于所有的 \(L_i\) 都同分布,所以对于 \(\forall i\in [n+1], \Pr{L_i>t}=(1-t)^n\)。
假设我们在圆环上均匀随机选两个点,这两个点把圆环分成了两个弧。很容易验证,每一条弧的平均长度是 \(\frac{1}{2}\)。我们现在先在圆环上事先画一个标记点,然后再随机选两个点,请问包含了标记点的那个弧平均有多长?现在,你应该有正确的直观了,这个弧长的平均值应该大于 \(\frac{1}{2}\)!
我们设这段弧长为 \(L\),我们来计算一下它的分布函数。我们可以想象从标记点把圆环割开形成一个 \([0,1]\) 线段,那么不包含标记点的那一段就对应了我们一开始所定义的 \(L_2\)。因此 \[ \Pr{L\le t} = \Pr{L_2>1-t} = t^2. \] 所以 \[ \E{L} = \int_0^1 \Pr{L>t}\d t = \int_0^1 1-t^2\d t = \frac{2}{3}. \]
随机分裂
假设有一个初始质量为 \(1\) 的物质,其每单位时间会独立的分裂一次。分裂的方式是变成两块,质量分别为原来的 \(p\) 和 \(1-p\) 倍,其中 \(p\) 是 \([0,1]\) 中的一个均匀数字。那么,当分裂了 \(n\) 次之后,一块物质质量的分布是怎么样的呢?
我们用 \(Z_n\) 表示分裂了 \(n\) 次之后一块的质量。那么 \(Z_0=1\) 并且 \(Z_n = \prod_{i=1}^n X_i\),其中 \(X_i\) 为取值为 \([0,1]\) 的独立随机变量。我们可以看到,如果令 \(Y_i = -\log X_i\),那么 \[ \log Z_n = \sum_{i=1}^n \log X_i = -\sum_{i=1}^n Y_i \] 是 \(n\) 个独立的随机变量之和。我们现在来看 \(Y_i\) 的分布。 \[ \Pr{Y_i\ge t} = \Pr{-\log X_i\ge t} = \Pr{X_i\le e^{-t}} = e^{-t}. \] 因此,\(Y\sim\!{Exp}(1)\)。于是 \[ \Pr{Z_n\le t} = \Pr{\sum_{i=1}^n Y_n\ge -\log t} = 1-G_n\tp{\log\tp{\frac{1}{t}}}. \] 这儿 \(G_n(x) = 1-e^{-x}\tp{\sum_{k=0}^{n-1} \frac{x^k}{k!}}\) 是速率为 \(1\) 的 \(\Gamma(n,1)\) 分布的分布函数。
顺序统计量的分布
我们把 \([0,1]\) 上随机扔的 \(n\) 个点按照大小顺序排好序的随机变量 \(X^{(1)},\dots,X^{(n)}\) 称为顺序统计量。我们来研究它的分布。我们用 \(F_k\) 表示 \(X^{(k)}\) 的分布函数,那么,简单思考之后可以看出来 \[ F_k(t) = \Pr{X^{(k)}\le t} = \sum_{j=k}^n \binom{n}{j}t^j(1-t)^{n-j}. \] 我们可以直接求导来得到 \(X^{(k)}\) 的概率密度函数 \(f_k\)。但这儿我们直接从导数的定义来看可以更容易的得到 \(f_k\) 的表达式。 \[ \begin{align*} f_k(t) &=\lim_{h\to 0} \frac{1}{h} \cdot \Pr{X^{(k)}\in [t,t+h]}\\ &=\lim_{h\to 0} \frac{1}{h} \cdot n\binom{n-1}{k-1} h\cdot (t+O(h))^{k-1}\cdot (1-t+O(h))^{n-k}\\ &=n\binom{n-1}{k-1}t^{k-1}(1-t)^{n-k}. \end{align*} \] 我们来考察 \(n X^{(k)}\) 的分布,这等价于我们把 \([0,1]\) scale 成 \([0,n]\), 并且 \(\E{n X^{(k)}} = k\cdot \frac{n}{n+1}\overset{n\to \infty}{\to} k\). \[ \Pr{nX^{(k)}>t} = \Pr{X^{(k)} > \frac{t}{n}} = \sum_{j=0}^{k-1}\binom{n}{j}\tp{\frac{t}{n}}^j\tp{1-\frac{t}{n}}^{n-j}\overset{n\to\infty}{\to} \sum_{j=0}^{k-1}\frac{t^j}{j!}e^{-t}. \] 注意到,这是 Gamma 分布 \(\Gamma(k,1)\) 的分布函数。换句话说,当 \(n\) 足够大的时候,\(n\cdot X^{(k)}\) 的分布会收敛到 \(\Gamma(k,1)\) 分布!
均匀分布的和与覆盖概率
我们现在考虑另外一个问题,假设 \(X_1,\dots,X_n\sim\!{Unif}([0,a])\) 是 \(n\) 个独立随机变量,那么它们的和 \(S_n=\sum_{i=1}^n X_i\) 的分布是什么样的呢?我们用 \(U_n\) 和 \(u_n\) 分别来表示 \(S_n\) 的分布函数和概率密度函数。我们可以使用全概率公式得到 \[ \begin{align*} u_1(x) &= \frac{1}{a},\quad x\in [0,a]\\ u_{n+1}(x) &= \frac{1}{a}\int_0^a u_n(x-y)\d y = \frac{1}{a}\tp{U_n(x)-U_n(x-a)}, \forall n\ge 1. \end{align*} \] 因此,\(u_n\) 具有所谓“卷积”形式的递推式。为了方便叙述,对于 \(x\in\bb R\),我们用 \(x_+\) 来表示 \(\max\set{x,0}\)。那么, \[ U_1(x) = a^{-1}\cdot (x_+-(x-a)_+). \] 我们接着证明
Theorem 1 \[ \begin{align*} U_n(x) &= \frac{1}{a^n n!}\sum_{j=0}^n (-1)^j\binom{n}{j}\tp{(x-j\cdot a)_+}^n\\ u_{n+1}(x) &= \frac{1}{a^{n+1}n!}\sum_{j=0}^{n+1}(-1)^j\binom{n+1}{j}\tp{(x-j\cdot a)_+}^n. \end{align*} \]
既然表达式都告诉你了,我们使用归纳法进行验证即可。边界条件 \(n=1\) 是容易验证的。对于更大的 \(n\),使用归纳假设和 Fubini-Tonelli,我们有 \[ \begin{align*} U_n(x) &=\int_0^x u_n(t)\d t\\ &=\frac{1}{a^n(n-1)!}\sum_{j=0}^n (-1)^j\binom{n}{j}\int_0^x (t-j\cdot a)_+^{n-1}\d t\\ &=\frac{1}{a^n n!}\sum_{j=0}^n (-1)^j\binom{n}{j}(x-j\cdot a)_+^n. \end{align*} \] 当 \(j\not\in\set{0,1,\dots,n}\) 时,按照惯例我们让 \(\binom{n}{j} = 0\)。这样我们在上面求和的时候,可以让 \(j\) 的取值范围是所有的整数。那么,我们有 \[ \begin{align*} u_{n+1}(x) &=a^{-1}\cdot \tp{U_n(x)-U_n(x-a)}\\ &=\frac{1}{a^{n+1} n!}\sum_{j\in \bb Z} (-1)^j\binom{n}{j}\tp{(x-j\cdot a)_+^n - (x-(j+1)\cdot a)_+^n}\\ &=\frac{1}{a^{n+1}n!}\sum_{j\in \bb Z}(-1)^j \tp{\binom{n}{j}+\binom{n}{j-1}}(x-j\cdot a)_+^n\\ &=\frac{1}{a^{n+1}n!}\sum_{j\in\bb Z} (-1)^j \binom{n+1}{j}(x-j\cdot a)_+^n. \end{align*} \] 我们使用上面的结论研究一个有趣的问题:往一个圆环上均匀随机扔 \(n\) 个长度为 \(a\) 的圆弧,有多大概率能够盖住整个圆环?这个问题在水源上也有人问过。
我们用 \(\varphi_n(t)\) 表示在长度为 \(t\) 的圆环上均匀扔 \(n\) 个长度为 \(a\) 的圆弧盖住圆环的概率。所谓 \(n\) 个圆弧盖住圆环,这等价于在 \([0,t]\) 的区间上扔 \(n-1\) 个点,使得相邻两个点(包括两个顶点)的距离不大于 \(a\)。简单思考一下,我们可以写出递推式 \[ \varphi_n(t) = (n-1)\int_0^a\varphi_{n-1}(t-x)\tp{\frac{t-x}{t}}^{n-2}\cdot \frac{1}{t}\d x. \] 注意到 \(\varphi_n(t)\) 的递推式也是“卷积”形式,和 \(u_n\) 有一点像。我们可以凑出 \(\varphi_n\) 和 \(u_n\) 的关系。实际上,我们可以验证, \[ \varphi_n(t) = a^n(n-1)!u_n(t)\frac{1}{t^{n-1}}. \]