第十八讲:随机变量收敛的模式,Borel-Cantelli 引理
随机变量的收敛(Convergence of Random Variables)
在概率论的研究里面,我们经常会讨论(定义在同一个概率空间上的)随机变量列 \(\set{X_n}_{n\ge 1}\) 收敛到 \(X\)。我们之前已经遇到过所谓的“几乎必然”收敛 \(X_n\overset{a.s.}{\to} X\)。我们今天将介绍其它几种常见的收敛模式。这些收敛模式会出现在概率论研究的不同场合。比如说,在这门课未来学习大数定律的时候我们会接触“依概率”收敛,在未来学习随机过程的时候会遇到“依 \(L^2\) ”收敛,以及我们在计算中常常用到的“依分布”收敛。我们现在先给出各自的定义,并研究互相之间的关系。
如果不特别说明,我们下面均设 \(\set{X_n}_{n\ge 1}\) 和 \(X\) 为概率空间 \((\Omega,\@F,\bb P)\) 上的随机变量。
几乎必然收敛 (almost surely convergence)
也叫做“以概率 \(1\) 收敛”,即存在一个可测集 \(\Omega'\subseteq\Omega\) 满足 \(\Pr{\Omega'} = 1\),并且 \(\forall \omega\in\Omega'\),\(\lim_{n\to\infty}X_n(\omega) = X(\omega)\)。我们可以等价的写作 \[ \Pr{\lim_{n\to\infty} X_n=X} = 1. \] 我们一般记作 \(X_n\overset{a.s.}{\to} X\). ### 依概率收敛(converge in probability)
指的是对于任何 \(\eps>0\), \[ \lim_{n\to\infty} \Pr{\abs{X_n-X}>\eps} = 0. \] 我们一般记作 \(X_n\overset{P}{\to} X\).
依 \(L^p\) 收敛(converge in \(L^p\) )
这里 \(p\ge 1\) 是一个整数。它的定义是 \[ \lim_{n\to\infty} \E{\abs{X_n-X}^p} = 0. \] 我们一般记作 \(X_n\overset{L^p}{\to} X\).
依分布收敛(converge in distribution)
依分布收敛和上述几种收敛模式不一样,它不要求这些随机变量生活在同一个概率空间中。我们可以假设 \(X_n\) 的分布函数是 \(F_n\),\(X\) 的分布函数是 \(F\)。它的定义是,对于每一个 \(F(x)\) 连续的点 \(x\),有 \[ \lim_{n\to\infty} F_n(x) = F(x). \] 我们一般记作 \(X_n\overset{D}{\to} X\).
收敛之间的关系
给出了这么多收敛的定义,小朋友一定有一堆疑问。为什么要有这么多不同种类的收敛?它们之间有什么关系?各自的直观又是什么?
对于第一个问题,我们在未来的学习中会逐渐体会到。但一个主要原因是,这些收敛有强有弱,我们关心的概率结论,在有的时候往往只能在比较弱的收敛意义下成立,或者在强的意义下成立需要更多的限制条件,或者更复杂的证明。我们现在来回答后两个问题。
我们假设 \(q\ge p\ge 1\) 是整数。我们在下图中展示了各个收敛模式的关系。
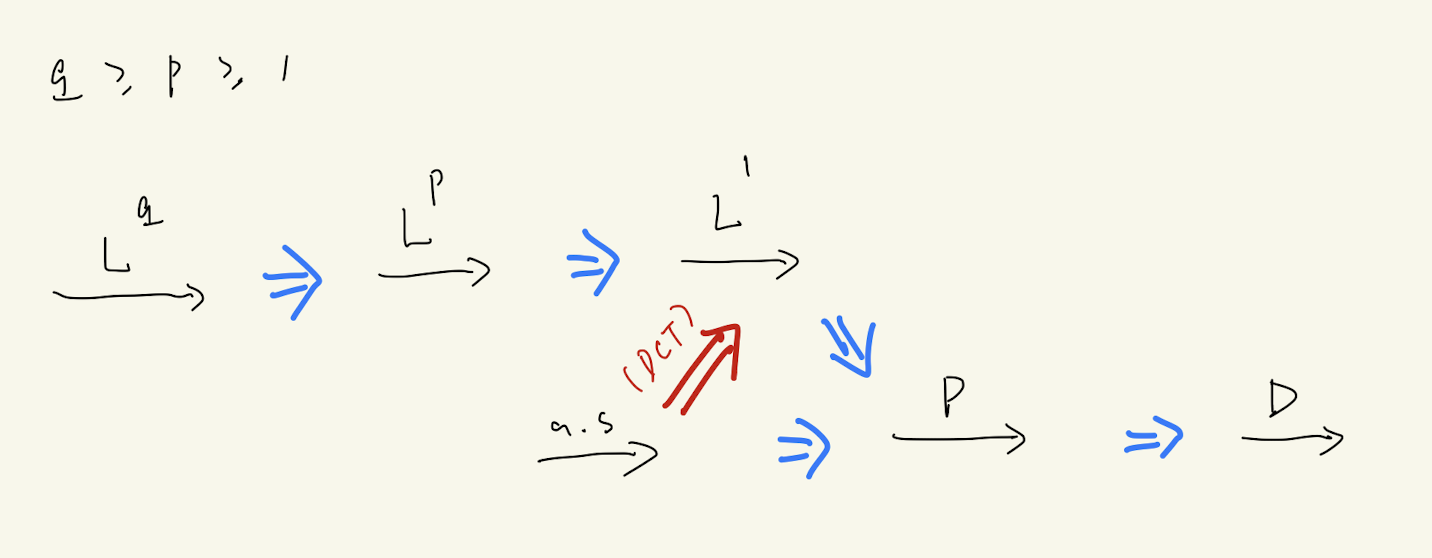
\(\overset{a.s}{\to}\) 与 \(\overset{P}{\to}\)
首先我们通过一个例子说明,\(\overset{P}{\to}\) 不能推出 \(\overset{a.s.}{\to}\)。这个例子如图所示:设 \(X_n\) 和 \(X\) 都是定义在 \([0,1]\) 的均匀测度上的随机变量,其中 \(X\equiv 0\)。对于任意的 \(n\ge 1\),我们设 \(m=\lceil\log_2(n+1)\rceil-1\)。则我们知道 \(n\in [2^m,2^{m+1}-1]\)。我们取 \(k = n-(2^m-1)\in [1,2^m]\)。我们定义 \[ X_n = \begin{cases} 1, & \mbox{$\omega \in [(k-1)\cdot 2^{-m},k\cdot 2^{-m})$}\\ 0, & \mbox{otherwise.} \end{cases} \]
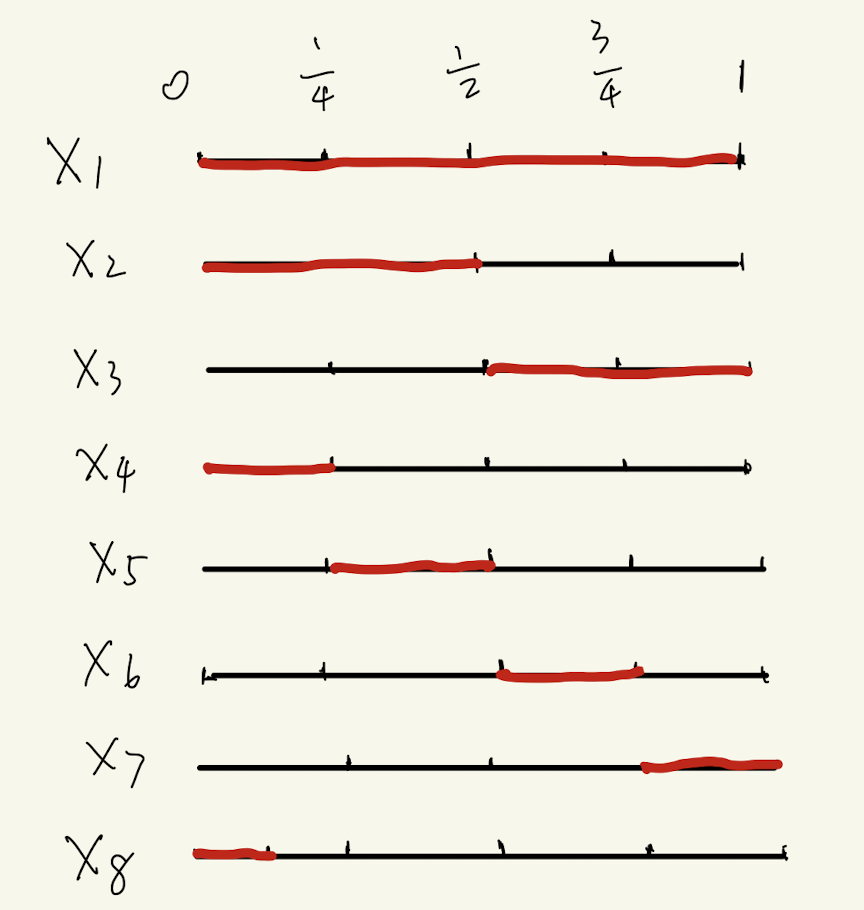
直观上说,我们让 \(X_n\) 在图中为红色的线段部份取值为 \(1\),其余的部分为 \(0\)。令 \(X=0\)。可以看出,红色部分是越来越少的,即 \(X_n\ne X\) 的测度越来越小。即 \[ \lim_{n\to\infty} \Pr{\abs{X_n-X}>\eps} = 0. \] 但是,显然我们有 \(X_n\overset{a.s}{\to} X\) 不成立。事实上,对于任意的 \(\omega\in [0,1]\),我们都有 \(X_n(\omega)\) 是不收敛的,因为红色的部分会无穷次的扫过 \(\omega\) 这个点。
这个反例很好的展示了这两种收敛模式的区别:即 \(X_n\) 与 \(X\) 不同的地方测度尽管越来越小,但是这个位置是可以移动,这种移动阻止了几乎处处收敛。
我们接着来说明,\(\overset{a.s.}{\to}\) 可以推出 \(\overset{P}{\to}\)。我们来证明, \[ X_n\overset{a.s}{\to} X \iff \forall \eps>0,\;\lim_{n\to\infty} \Pr{\sup_{k\ge n} \abs{X_k-X}>\eps} = 0. \] 由于 \(\abs{X_n-X}>\eps\implies \sup_{k\ge n} \abs{X_k-X}>\eps\),所以说明了 \(X_n\overset{P}{\to} X\)。对于每一个 \(n\), 我们定义 \(Z_n = \sup_{k\ge n} \abs{X_k-X}\)。注意到 \[ \begin{align*} X_n\overset{a.s}{\to} X &\iff \exists \Omega'\subseteq\Omega \mbox{ s.t. } \Pr{\Omega'}=1 \mbox{ and }\forall \omega\in \Omega',\;X_n(\omega)\to X(\omega)\\ &\iff \exists \Omega'\subseteq\Omega \mbox{ s.t. } \Pr{\Omega'}=1 \mbox{ and }\forall \omega\in\Omega',\;Z_n(\omega)\to 0\\ &\iff \forall \eps\in\bb Q_{>0}, \exists \Omega'\subseteq\Omega \mbox{ s.t. } \Pr{\Omega'}=1 \mbox{ and }\forall \omega\in\Omega',\;\lim_{n\to\infty} Z_n(\omega)\le \eps\\ &\iff \forall \eps\in\bb Q_{>0}, \Pr{\lim_{n\to\infty}\set{\omega\cmid Z_n(\omega)>\eps}}=0\\ &\iff \forall \eps>0, \lim_{n\to\infty} \Pr{Z_n>\eps}=0. \end{align*} \]
\(\overset{L^p}{\to}\) 与 \(\overset{P}{\to}\)
我们接着说明,对于 \(p\ge 1\),“依 \(L^p\) 收敛”可以推出“依概率收敛”,但是反过来不成立。我们只需要对 \(p=1\) 的情况进行证明,因为,我们接着马上要说明,如果 \(p>1\),那么“依 \(L^p\) 收敛”可以推出“依 \(L^1\) 收敛”。
这件事情正确的直观也很容易,“依概率收敛”是说的随机变量 \(X_n\) 和 \(X\) 不一样的位置的测度趋向于 \(0\)。而“依 \(L^p\) 收敛”要求的是在不一样的地方,这个测度还要乘上“两者所差”的值之后依旧趋向于 \(0\)。因此,这个要求更强一些。证明使用马尔可夫不等式即可:对于任何 \(\eps>0\), \[ \lim_{n\to\infty} \Pr{\abs{X_n-X}>\eps}\le \lim_{n\to\infty} \frac{\E{\abs{X_n-X}}}{{\eps}} = 0. \] 反过来不成立的例子是我们很熟悉的:设 \(X_n\), \(X\) 均是定义在 \((0,1)\) 的均匀测度上的随机变量。我们令 \(X_n = n\cdot\bb I_{(0,\frac{1}{n})}\),\(X=0\)。
\(\overset{L^q}{\to}\) 与 \(\overset{L^p}{\to}\)
和上面相同的直观指出,如果 \(q>p\),那么 \(X_n\overset{L^q}{\to} X\) 可以推出 \(X_n\overset{L^p}{\to} X\)。证明如下: \[ \lim_{n\to\infty} \E{\abs{X_n-X}^p} = \lim_{n\to\infty} \E{\tp{\abs{X_n-X}^q}^{\frac{p}{q}}}\le \lim_{n\to\infty}\tp{\E{\abs{X_n-X}^q}}^{\frac{p}{q}} = 0. \] 其中上式的不等号是利用琴生不等式以及 \(f(x) = x^{\frac{p}{q}}\) 是一个 concave 函数的事实。
反过来不成立的例子可以类似前一种情况给出,留作练习(
\(\overset{P}{\to}\) 与 \(\overset{D}{\to}\)
根据定义就可以知道,“依分布收敛” \(\overset{D}{\to}\) 是一个很弱的概念,它关心的是分布函数的收敛性,甚至都不要求随机变量们生活在同一个概率空间上。
固定概率空间 \((\Omega,2^\Omega,\bb P)\) 为在 \(\Omega=\set{0,1}\) 上的均匀分布。对于任意 \(n\), 定义 \(X_n(0)=0, X_n(1)=1\)。定义 \(X(0)=1, X(1)=0\)。那显然 \(X_n\overset{D}{\to} X\) 但是 \(X_n\not\overset{P}{\to} X\).
我们现在来说明 \(X_n\overset{P}{\to}X\) 可以推出 \(X_n\overset{D}{\to} X\)。我们想把事件 \(\abs{X_n-X}>\eps\) 与 \(X_n\) 的分布函数联系起来。我们使用下面一个基本的事实:对于任意 \(\eps>0\),任意两个随机变量 \(X,Y\) 和实数 \(a\): \[ Y\le a \implies X\le a+\eps \mbox{ or } \abs{Y-X}>\eps, \] 即如果已知 \(Y\) 不大于 \(a\),则要么 \(X\) 不大于 \(a+\eps\),要么 \(X\) 和 \(Y\) 的差距比较大。我们使用这个不等式两次,并使用 union-bound,可以得到 \[ \begin{align*} \Pr{X_n\le a} &\le \Pr{X\le a+\eps} + \Pr{\abs{X_n-X}>\eps}\\ \Pr{X<a-\eps} &\le \Pr{X_n\le a}+ \Pr{\abs{X_n-X}>\eps} \end{align*} \] 这便得到了 \[ \Pr{X\le a-\eps}-\Pr{\abs{X_n-X}>\eps}\le \Pr{X_n\le a}\le \Pr{X\le a+\eps}+\Pr{\abs{X_n-X}>\eps}. \] 我们让 \(n\) 趋向于无穷大并让 \(\eps\to 0\) 便得到了想要的结论。
\(\overset{a.s.}{\to}\) 与 \(\overset{L^1}{\to}\)
这两者一般来说是不可比较的。事实上,在一定条件下,我们有 \(X_n\overset{a.s.}{\to} X \implies X_n\overset{L^1}{\to} X\)。如果我们存在一个可积的随机变量 \(Y\),满足对于每一个 \(n\),\(\abs{X_n}\le Y\) 并且 \(\abs{X}\le Y\)。那么 容易验证 \(\abs{X_n-X}\le 2Y\)。显然我们也有 \(\abs{X_n-X}\overset{a.s.}{\to}0\)。因此由 DCT \[ \lim_{n\to\infty} \E{\abs{X_n-X}} = \E{\lim_{n\to\infty}\abs{X_n-X}} = 0. \]
集合的极限
我们之前定义过集合的极限的概念。如果 \(\set{A_n}_{n\ge 1}\) 是单调递增的( \(\forall n, A_n\subseteq A_{n+1}\) ),那么 \[ \lim_{n\to\infty} A_n \defeq \bigcup_{n\ge 1}A_n. \] 类似的,如果 \(\set{A_n}_{n\ge 1}\) 是单调递减的( \(\forall n, A_n\supseteq A_{n+1}\) ),那么 \[ \lim_{n\to\infty} A_n\defeq \bigcap_{n\ge 1}A_n. \] 这可以类比于数列的极限。假设我们有一列实数 \(a_n\),如果它是单调的数列,那么它一定存在极限(允许极限是正负无穷大的话)。而如果数列不单调的话,那么极限就不一定存在了。但是,我们可以定义它的上极限和下极限: \[ \begin{align*} \limsup_{n\to\infty} a_n &\defeq \lim_{n\to\infty}\tp{\sup_{k\ge n} a_k}\\ \liminf_{n\to\infty} a_n &\defeq \lim_{n\to\infty}\tp{\inf_{k\ge n} a_k}. \end{align*} \] 上极限和下极限总是存在的,这是因为 \(\tp{\sup_{k\ge n} a_k}_{n\ge 1}\) 与 \(\tp{\inf_{k\ge n} a_k}_{n\ge 1}\) 分别是单调递减和单调递增的数列。我们尝试类似的定义集合列的上极限与下极限。设 \(\tp{A_n}_{n\ge 1}\) 是一列(不一定单调的)集合。我们定义 \[ \begin{align*} \limsup_{n\to\infty} A_n &\defeq \lim_{n\to\infty}\tp{\sup_{k\ge n} A_k}\\ \liminf_{n\to\infty} A_n &\defeq \lim_{n\to\infty}\tp{\inf_{k\ge n} A_k}. \end{align*} \] 当然,我们还没有说 \(\sup_{k\ge n} A_k\) 和 \(\inf_{k\ge n} A_k\) 是怎么定义的。但是,我们可以很自然的想到,对于一个集族 \(\set{B_n}_{n\in I}\),其上确界应该是包含每一个 \(B_n\) 的最小的集合,而下确界应该是被每一个 \(B_n\) 包含的最大的集合。因此 \[ \begin{align*} \sup_{n\in I} B_n &\defeq \bigcup_{n\in I} B_n\\ \inf_{n\in I} B_n &\defeq \bigcap_{n\in I} B_n. \end{align*} \] 使用这个定义,以及对于单调集合族极限的定义,我们有: \[ \begin{align*} \limsup_{n\to\infty} A_n &\defeq \lim_{n\to\infty}\tp{\sup_{k\ge n} A_k} = \bigcap_{n\ge 1}\bigcup_{k\ge n} A_k\\ \liminf_{n\to\infty} A_n &\defeq \lim_{n\to\infty}\tp{\inf_{k\ge n} A_k} = \bigcup_{n\ge 1}\bigcap_{k\ge n} A_k. \end{align*} \] 另外一个比较重要的事情是我们来看看 \(\limsup A_n\) 和 \(\liminf A_n\) 究竟包含的哪些元素。简单的思考之后(记得思考哦),我们可以发现 \[ \begin{align*} \limsup A_n &= \set{x\cmid x\mbox{ 在无穷多个 }A_n\mbox{ 中出现过}},\\ \liminf A_n &= \set{x\cmid x\mbox{ 只在有限个 }A_n\mbox{ 中没出现过}}. \end{align*} \] 基于这种直观含义,我们有的时候会把 “ \(\limsup A_n\) ” 记作 “ \(A_n\) i.o”,其中“i.o”是 “infinitely often” 的意思。
我们使用定义以及集合的 De-Morgan 律,可以马上得到 * \(\limsup A_n = \tp{\liminf A_n^c}^c\).
波莱尔-坎泰利引理 (Borel-Cantelli Lemma)
我们接着介绍一个很常用的工具。它通常处理的问题是这样的:假设在一个固定的概率空间里,我们有一些坏事件 \(\set{A_n}_{n\ge 1}\)。我们想知道,有多大的概率,这些坏事件不会总发生。
Lemma 1 (Borel-Cantelli) 如果 \(\sum_{n\ge 1} \Pr{A_n}<\infty\),那么 \(\Pr{A_n\mbox{ i.o}} = 0\).
我们前面刚说过 \[ A_n \mbox{ i.o } = \limsup_n A_n = \set{\omega\cmid \omega\mbox{ 在无穷多个 }A_n\mbox{ 中出现过}}. \] 因此,Borel-Cantelli 说的是,如果所有的坏事件(它们可能互相相关)发生的概率之和是一个有限数的话,那么,几乎一定(almost surely)这些坏事件不会不停发生。
Borel-Cantelli 的证明非常简单: \[ \Pr{A_n\mbox{ i.o}} = \Pr{\lim_n\tp{\sup_{k\ge n} A_k}} = \lim_{n}\Pr{\sup_{k\ge n} A_k}\le \lim_n\sum_{k\ge n}\Pr{A_k}. \] 上面式子里第二个等号是因为概率测度的连续性,不等号是使用了 union-bound。根据我们的条件,\(\sum_{n\ge 1}\Pr{A_n}<\infty\),而一个收敛级数的 tail 一定是 \(0\)。所以我们有 \(\Pr{A_n\mbox{ i.o}} = 0\).
Borel-Cantelli 反过来就不一定正确了,也就是说如果 \(\sum_{n\ge 1} \Pr{A_n} = \infty\),不一定有 \(\Pr{A_n\mbox{ i.o}}>0\)。但是,如果这些坏事件是相互独立的,那么 \(\Pr{A_n\mbox{ i.o}}=1\)。这个结论又被称为第二 Borel-Cantelli 引理。
Lemma 2 (Second Borel-Cantelli) 如果 \(A_n\) 相互独立,那么
- \(\Pr{A_n\mbox{ i.o.}} = 0 \iff \sum_{n\ge 1}\Pr{A_n}<\infty\).
- \(\Pr{A_n\mbox{ i.o.}} = 1 \iff \sum_{n\ge 1}\Pr{A_n}=\infty\).
这个引理也说明,概率 \(\Pr{A_n\mbox{ i.o.}}\) 只有 \(0\) 或者 \(1\) 两种取值。这实际上是一种更一般的现象,被称为 \(0\)-\(1\) 律,我们在未来会介绍。
我们现在证明 Second Borel-Cantelli。事实上,我们只要证明 \(\sum_{n\ge 1} \Pr{A_n}=\infty\implies \Pr{A_n\mbox{ i.o.}}=1\) 就可以了(why)。于是,我们利用独立的条件和 De-Morgen 律可以得到 \[ \Pr{\limsup_n A_n}=1-\Pr{\liminf_n A_n^c}=1-\lim_n\Pr{\bigcap_{k\ge n} A_k^c}=1-\lim_n \prod_{k\ge n}\Pr{A_k^c}. \] 如果我们设 \(x_k\defeq \Pr{A_k}\),那么 \[ \Pr{\limsup_n A_n}=1-\lim_n \prod_{k\ge n}(1-x_k)\ge 1-\lim_n e^{-\sum_{k\ge n} x_k}=1. \] 其中最后一个等号是因为 \(\sum_{n} x_n=\infty\) 是一个发散的级数(因此它的 tail 是发散的)。
我们现在来使用 Borel-Cantelli 来证明一个有用的结论。即如果 \(X_n\overset{P}{\to} X\),那么存在一个子序列 \(n_1,n_2,\dots\),满足 \(X_{n_k}\overset{a.s.}{\to} X\)。
大家可以先想想,在我们前面说明 \(X_n\overset{P}{\to} X\not\overset{a.s.}{\to} X\) 的例子里,这样一个子序列如何挑。
我们只用挑那些红色都在最左边的 \(X_{n_k}\) 即可。
以下的证明,是 Borel-Cantelli 引理的一个典型应用。对于每一个 \(k\ge 1\),我们选取 \(n_k\) 满足 \(\Pr{\abs{X_{n_k}-X}\ge \frac{1}{k}}\le \frac{1}{2^k}\)。由于 \(X_n\overset{P}{\to} X\),这样的 \(n_k\) 总是可以挑出来。我们用 \(A_k\) 来表示坏事件“ \(\abs{X_{n_k}-X}\ge \frac{1}{k}\) ”。那么根据定义 \(\sum_{k\ge 1}\Pr{A_k} \le \sum_{k\ge 1} 2^{-k}<\infty\)。于是使用 Borel-Cantelli,我们可以得到 \(\Pr{A_n\mbox{ i.o.}} = 0\)。
我们需要仔细解读一下 \(\Pr{A_n\mbox{ i.o.}}=0\) 意味着什么。它说明,存在 \(\Omega'\subseteq\Omega\),满足 \(\Pr{\Omega'}=1\),对于任何 \(\omega\in\Omega'\),只存在有限个 \(k\),使得 \(\abs{X_{n_k}(\omega)-X(\omega)}\ge \frac{1}{k}\) 成立。这意味着对于每一个这样的 \(\omega\in \Omega'\),\(X_{n_k}(\omega)\to X(\omega)\)。
我们可以使用这个结论加强我们的老熟人控制收敛定理:
Theorem 1 设 \(X_n\) 为一列随机变量,满足 \(\lim_{n\to\infty} X_n = X\;a.e.\)。如果存在一个随机变量 \(Y\),满足
- 对所有 \(n\in\bb N\),\(\abs{X_n}\le Y\);
- \(\E{Y}<\infty\) 是可积的。
那么 \(\lim_{n\to\infty}\E{X_n}=\E{X}\)。
我们现在说明,我们可以把条件里的 \(X_n\overset{a.s.}{\to} X\) 弱化成 \(X_n\overset{P}{\to}X\)。我们使用反证法。假设 \(\lim_n \E{X_n} = \E{X}\) 不成立。那么,一定存在一个子序列 \(\set{n_k}_{k\ge 1}\) 满足 \(\lim_{k\to\infty} \E{X_{n_k}} = L\ne \E{X}\)。根据条件,我们知道 \(X_{n_k}\overset{P}{\to} X\)。因此,使用我们刚才证明的结论,从 \(\set{n_k}_{k\ge 1}\) 中我们能再找到一个子序列 \(\set{m_j}_{j\ge 1}\subseteq \set{n_k}_{k\ge 1}\),满足 \(X_{m_j}\overset{a.s.}{\to} X\)。根据 a.s. 版本的 DCT,我们知道 \(\lim_{j\to\infty} \E{X_{m_j}} = \E{X}\ne L\),这与 \(\set{X_{m_j}}\) 是 \(\set{X_{n_k}}\) 的子序列矛盾,因为 \(\E{X_{m_j}}\) 与 \(\E{X_{n_k}}\) 理应有一样的极限。