第二十二讲：依分布收敛，棣莫弗-拉普拉斯中心极限定理

中心极限定理的动机

我们之前讨论了大数定律，其想说的事情是给定一系列随机变量 \(X_1,X_2,\dots\)，如果每一个 \(X_i\) 的期望均是 \(\mu\)，那么在某些条件下，其部分和 \(S_n = \sum_{i\in [n]} X_i\) 满足 \(\frac{S_n}{n}\) 会收敛到 \(\mu\)。注意到，每一个 \(\frac{S_n}{n}\) 都是一个随机变量，而 \(\mu\) 本身是一个固定数（常值随机变量）。为什么随机变量会收敛到一个固定的数呢？如果我们再假设每一个 \(X_i\) 满足 \(\Var{X_i}\le \sigma^2\)，并且它们是相互独立的，那么我们知道 \[ \Var{\frac{S_n}{n}} = \frac{\sum_{i=1}^n\Var{X_i}}{n^2}\le \frac{\sigma^2}{n}\to 0. \] 也就是说，我们把 \(S_n\) 除 \(n\) 的操作使得当 \(n\) 足够大时，\(\frac{S_n}{n}\) 的方差趋向于零了，因此，其也自然的收敛到一个常数。

一个很自然的问题是，对于任意一个关于 \(n\) 的递增函数 \(f(n)\)，随机变量 \(\frac{S_n}{f(n)}\) 的收敛情况是怎么样的呢。简单计算就知道，当 \(f(n) = \omega(\sqrt{n})\) 的时候，\(\Var{\frac{S_n}{f(n)}}\) 同样收敛到 \(0\)；而当 \(f(n) = o(\sqrt{n})\) 的时候，其方差会趋向于无穷大。对于这样的 \(f(n)\)，有一些有趣的性质可以讨论（我们在作业中会遇到），但最有意思的事情发生在 \(f(n)=\sqrt{n}\) 的时候，这便是中心极限定理所讨论的问题。

我们先严格化我们的设定。假设 \(X_1,X_2,\dots\) 是定义在同一个概率空间上的独立同分布的随机变量，满足 \(\E{X_1}=\mu\)，\(\Var{X_1}=\sigma^2\) 均是有限的。我们关心 \(\frac{S_n}{\sqrt{n}}\) 的极限行为。我们首先证明一个有一些惊人的结论：

Proposition 1 如果 \(\E{X_1}=0\) 并且 \(\E{X_1^4}<\infty\)，那么不存在一个随机变量 \(X\) 使得 \(\frac{S_n}{\sqrt{n}}\overset{P}{\to} X\)。

我们假设这样一个 \(X\) 存在。前面的课上证明过 \(\frac{S_n}{\sqrt{n}}\overset{P}{\to} X\) 可以推出一定存在一个子序列 \(\set{n_j}\) 满足 \(\frac{S_{n_j}}{\sqrt{n_j}}\overset{a.s.}{\to} X\)。由于我们知道对于每一个 \(j\)，\(\E{\frac{S_{n_j}}{\sqrt{n_j}}} = 0\) 并且 \(\Var{\frac{S_{n_j}}{\sqrt{n_j}}}=\sigma^2\)。下面的引理可以保证 \(X\) 一定也满足 \(\E{X} = 0\)，\(\Var{X}=\sigma^2\)。这是一个类似 DCT 和 MCT 的 yet another 保证极限和期望可以交换的充分条件，我们把它的证明放在本次讲义最后（事实上，极限和期望交换的充要条件是所谓的“一致可积（uniform integrability）”，因为课时原因我们不再介绍）。

Lemma 1 设 \(X_1,X_2,\dots\) 是一族随机变量满足 \(X_n\overset{a.s}{\to} X\)。如果存在 \(\eps>0\) 和常数 \(M\)，使得对于每一个 \(n\)， \(\E{\abs{X_n}^{1+\eps}}\le M\)，那么 \[ \lim_{n\to\infty} \E{X_n} = \E{X}. \]

但是另一方面，我们知道 \(X\) 是一个所谓的“尾变量”，也就是说，对于任何 Borel 集 \(B\in \@B(\bb R)\)，事件 \([X\in B]\) 都是 \(\@F^*_\infty\) 中的一个尾事件，这儿显然 \(\@F_n = \sigma(X_1,\dots,X_n)\)。根据 Kolmogorov 0-1 律，\([X\in B]\) 发生的概率要么是 \(0\) 要么是 \(1\)。这也说明 \(X\) 一定等于某一个常数。但这与它的方差是 \(\sigma^2>0\) 矛盾。

上面的讨论说明，我们不能期待对于 \(\frac{S_n}{\sqrt{n}}\) 在依概率收敛或者几乎处处收敛的意义上说什么。我们考虑一个更弱的收敛定义，即依分布收敛。回忆我们之前定义过的依分布收敛：设 \(X_1,X_2,\dots\) 分别有分布函数 \(F_n\)，并且 \(X\) 有分布函数 \(F\)。我们说 \(X_n\overset{D}{\to} X\) 当且仅当对于 \(F\) 的每一个连续的点 \(x\)，有 \(\lim_{n\to\infty} F_n(x) = F(x)\)。最基本的中心极限定理便是如下结论：

Theorem 1 如果独立同分布的随机变量 \(X_1,X_2,\dots\) 满足 \(\E{X_1}=\mu, \Var{X_1}=\sigma^2\) 均为有限的，那么 \[ \frac{S_n-n\mu}{\sigma\sqrt{n}}\overset{D}{\to} Y\sim\+N(0,1). \]

换句话说，如果我们把 \(X_i\) 归一化成期望为 \(0\) 方差为 \(1\) 的随机变量（即 \(X_i' = \frac{X_i-\mu}{\sigma}\) ），并令 \(S_n'=\sum_{i=1}^n X_i'\) 为归一化后的部分和。那么 \(\frac{S_n'}{\sqrt{n}}\) 依分布收敛到标准正态分布。 \[ \frac{\sum_{i=1}^n X_i'}{\sqrt{n}}\overset{D}{\to} Y\sim\+N(0,1). \]

相比大数定律，我认为这是一个非常让人意外的结果，因为它并没有对 \(X_i\) 的分布有要求，只规定了它的期望和方差。而中心极限定理告诉我们，不管 \(X_i\) 本身的分布是什么，当足够多的独立的 \(X_i\) 加在一起的时候，一定呈现出正态分布的样子。这也是正态分布在我们生活中经常出现的原因。

棣莫弗-拉普拉斯中心极限定理（De Moivre–Laplace theorem）

我们今天先证明一个简单版本的中心极限定理，即当每一个 \(X_i\) 都具有独立同分布的伯努利分布的情形。它被称作棣莫弗-拉普拉斯中心极限定理。我们证明的方法也很暴力，就是直接计算并估计 \(\frac{S_n}{\sqrt{n}}\) 的分布函数。在这个证明中使用的一些估计技巧是非常有用并且常见的。

我们严格的陈述一下要证明的结论。设 \(X_1,X_2,\dots\) 是独立的满足 \(\!{Ber}(p)\) 分布的随机变量，其中 \(p\in (0,1)\) 是一个常数，那么 \[ \frac{S_n-pn}{\sqrt{(p-p^2)n}} \overset{D}{\to} Y\sim \+N(0,1). \] 为了方便，我们只证明 \(p=\frac{1}{2}\) 的情况，对于一般的 \(p\) 可以完全类似的证明。

回忆我们用 \(\phi(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\) 来表示标准正态分布 \(\+N(0,1)\) 的概率密度函数。事实上，我们知道 \(S_n\) 是满足 \(\!{Binom}(n,\frac{1}{2})\) 分布的。因此，我们可以直接计算出它的概率质量函数 \(p_n(k) \defeq \Pr{S_n=k} = \binom{n}{k}2^{-n}\)。我们实际上想证明的是，当 \(n\) 足够大的时候，\(p_n(k)\) 所决定的离散的点列（图1），和 \(\phi(x)\) 对应的曲线（图2），在做适当放缩之后是逐渐趋向于一致的（图3）。

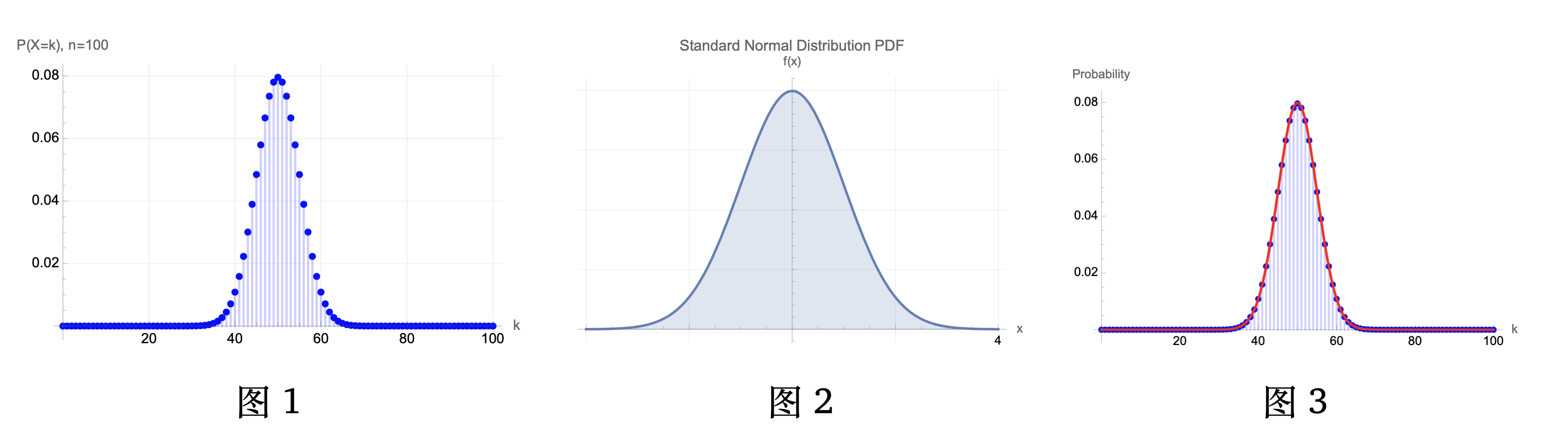
便让我们来严格证明这件事情。我们首先说明，当 \(k\) 比较接近其平均值 \(\frac{n}{2}\) 时， \(p_n(k)\) 的值和进行合适放缩后的 \(\phi\) 的值的差距是非常小的。

Lemma 2 设 \(C>0\) 是一个常数。那么 \[ \max_{\abs{k-n/2}\le C\cdot \sqrt{n}} \abs{\frac{p_n(k)\cdot \sqrt{n/4}}{\phi\tp{\frac{k-n/2}{\sqrt{n/4}}}}-1} = \+O\tp{n^{-1}}. \]

我们先解释一下上面引理里是如何缩放 \(\phi(x)\) 的。对于 \(k\sim\!{Binom}(n,\frac{1}{2})\)，我们知道其期望是 \(n/2\)，方差是 \(n/4\)。因此 \(\frac{k-n/2}{\sqrt{n/4}}\) 就是一个期望为 \(0\) 方差为 \(1\) 的随机变量，所以 \(p_n(k)\) 应该是和 \(\phi\tp{\frac{k-\frac{n}{2}}{\sqrt{n/4}}}\) 相比较。但此时，我们需要把它除掉 \(\sqrt{n/4}\) 才能保证其（对 \(k\) 的）积分为 \(1\)。

我们证明引理的主要工具就是斯特林公式：\(n! = \sqrt{2\pi n}\tp{\frac{n}{e}}^n\tp{1+\+O\tp{n^{-1}}}\)。使用这个公式以及 \(k\approx \frac{n}{2}\) 的事实，我们可以得到 \[ \begin{align*} p_n(k) &=\binom{n}{k}2^{-n}\\ &=\frac{n!}{k!(n-k)!}2^{-n}\\ &=\frac{\sqrt{2\pi n}}{\sqrt{2\pi k}\sqrt{2\pi (n-k)}} \frac{n^n}{k^k(n-k)^{n-k}}\cdot 2^{-n}\cdot\tp{1+\+O\tp{n^{-1}}}\\ &=\frac{1}{\sqrt{2\pi n}}\cdot \frac{1}{\sqrt{k/n}\cdot \sqrt{1-k/n}}\cdot \frac{2^{-n}}{\tp{k/n}^k\tp{1-k/n}^{n-k}}\cdot\tp{1+\+O\tp{n^{-1}}}. \end{align*} \] 我们的目标是把上式和 \(\phi\tp{\frac{k-n/2}{\sqrt{n/4}}} = \exp\tp{-\frac{1}{2n}\cdot (2k-n)^2}\) 进行比较。我们的策略如下：我们知道 \(k\approx \frac{n}{2}\)，所以我们把分母凑出形如 \(2k/n\approx 1\) 的项，然后尝试把这些接近于 \(1\) 的项用 \(1+x\approx e^x\) 换成指数形式，并期待能够变成 \(\phi(\cdot)\) 的形式。因此，我们可以继续变形得到 \[ \begin{align*} p_n(k) &=\sqrt{\frac{2}{\pi n}} \cdot \frac{1}{\sqrt{1+\frac{2k-n}{n}}\cdot\sqrt{1-\frac{2k-n}{n}}} \cdot \frac{1}{\tp{1+\frac{2k-n}{n}}^k\cdot \tp{1-\frac{2k-n}{n}}^{n-k}}\cdot\tp{1+\+O\tp{n^{-1}}}. \end{align*} \] 注意到，我们目标 \(\phi(\cdot)\) 里出现的是形如 \(e^{-(2k-n)^2}\) 的项，其指数上关于 \((2k-n)\) 的依赖是二次的。我们仅仅使用 \(1\pm x \approx e^{\pm x}\) 这个一阶近似是不够的，所以我们来计算 \(1\pm x\) 的二阶近似。

事实上我们注意到由于 \(k\approx n/2\)，所以 \(\tp{1+\frac{2k-n}{n}}^k\cdot \tp{1-\frac{2k-n}{n}}^{n-k} \approx \tp{1-\tp{\frac{2k-n}{n}}^2}^k\approx e^{-k\tp{\frac{2k-n}{n}}^2}\)。直接估计这儿 \(\approx\) 的误差也可以，但我认为下面的技巧更有通用性。

使用 \(\log (1+x)=x-\frac{x^2}{2}+\+O\tp{x^3}\)，我们有 \(1+x = e^{\log\tp{1+x}} = e^{x-\frac{x^2}{2}}\cdot \tp{1+\+O\tp{\abs{x}^3}}\)。注意我们这里要利用 \(\abs{k-\frac{n}{2}}=C\cdot \sqrt{n}\) 仔细估计误差项。可以得到 \[ p_n^k = \sqrt{\frac{2}{\pi n}}\cdot e^{\frac{1}{2}\cdot \tp{\frac{2k-n}{n}}^2}\cdot e^{-\frac{1}{2}\cdot \frac{(2k-n)^2}{n}}\tp{1+\+O\tp{n^{-1}}} = \sqrt{\frac{2}{\pi n}}\cdot e^{-\frac{1}{2}\cdot \frac{(2k-n)^2}{n}}\cdot \tp{1+\+O\tp{n^{-1}}}. \] 而这正是 \(\frac{\phi\tp{\frac{k-n/2}{\sqrt{n/4}}}}{\sqrt{n/4}}\tp{1+\+O\tp{n^{-1}}}\)。

设 \(F_n\) 是 \(\frac{S_n-\frac{n}{2}}{\sqrt{n/4}}\) 的分布函数。我们接下来只需要说明（why?）对于任何固定的常数 \(a<b\in \bb R\)，我们有 \(\lim_{n\to\infty} F_n(b)-F_n(a) = \int_{a}^b \phi(x)\dd x\)。

注意到 \[ \begin{align*} \abs{F_n(b)-F_n(a)-\int_a^b\phi(x)\dd x} &\le \abs{F_n(b)-F_n(a) - \sum_{k\in \bb N\colon a\le \frac{k-n/2}{\sqrt{n/4}}\le b}\frac{\phi\tp{\frac{k-n/2}{\sqrt{n/4}}}}{\sqrt{n/4}}}\\ &\quad +\abs{\sum_{k\in \bb N\colon a\le \frac{k-n/2}{\sqrt{n/4}}\le b}\frac{\phi\tp{\frac{k-n/2}{\sqrt{n/4}}}}{\sqrt{n/4}} - \int_a^b\phi(x)\dd x} \end{align*} \] 上式前一项的求和里最多有 \(\+O(\sqrt{n})\) 项，根据我们前面证明的引理，这一项带来的误差是 \(\frac{1}{\sqrt{n}}\) 级别。而上式第二项实际上是给出了积分和它的黎曼和的差，因此在 \(n\) 趋向于无穷大的时候趋向于 \(0\)。这便证明了我们的结果。 🎉🎉🎉

省略的证明

我们现在来证明

Lemma 3 设 \(X_1,X_2,\dots\) 是一族随机变量满足 \(X_n\overset{a.s}{\to} X\)。如果存在 \(\eps>0\) 和常数 \(M\)，使得对于每一个 \(n\)， \(\E{\abs{X_n}^{1+\eps}}\le M\)，那么 \[ \lim_{n\to\infty} \E{X_n} = \E{X}. \]

这个证明来自这个 notes。

对于任意 \(m>0\) 和随机变量 \(Y\)，我们定义一个新的随机变量 \[ Y^{[m]}(\omega) \defeq \begin{cases} m & \mbox{ if }Y(\omega)>m\\ -m & \mbox{ if }Y(\omega)<-m\\ Y(\omega) & \mbox{ if }Y(\omega)\in [m,-m]. \end{cases} \] 即 \(Y^{[m]}\) 把 \(Y\) 大于 \(m\) 和小于 \(-m\) 的部分分别换成 \(m\) 和 \(-m\)。于是 \(\abs{Y^{[m]}}\le m\)。根据 DCT，我们显然有 \[ \lim_{n\to\infty} \E{X_n^{[m]}} = \E{X^{[m]}}. \] 根据定义，我们又有 \[ \abs{X_n-X_n^{[m]}} \le \tp{\frac{\abs{X_n}}{m}}^\eps \abs{X_n} = m^{-\eps}\abs{X_n}^{1+\eps}. \] 于是，\(\E{X_n}=\E{X_n^{[m]}}\pm \+O\tp{m^{-\eps}M}\)。

根据 Fatou 引理，我们有 \[ \E{\abs{X}^{1+\eps}} \le \E{\liminf\abs{X_n}^{1+\eps}} \le \liminf\E{X_n^{1+\eps}}=M. \] 所以我们使用类似的推理可以得到 \[ \E{X} = \E{X^{[m]}}\pm \+O\tp{m^{-\eps}M}. \] 于是 \[ \limsup_{n\to\infty} \E{X_n}, \liminf_{n\to\infty}\E{X_n} = \lim_{n\to\infty} \E{X_n^{[m]}}\pm \+O\tp{m^{-\eps}M} = \E{X}\pm \+O\tp{m^{-\eps}M}. \] 令 \(m\to\infty\) 便得证。