第二十五讲：随机变量的特征函数

特征函数的定义以及基本性质

我们之前介绍过随机变量 \(X\) 的矩生成函数 \(M_X(t) = \E{e^{tX}}\)。它是研究随机变量的矩的有力工具。我们证明过的一个重要的性质是如果 \(M_X(t)\) 在 \(t=0\) 附近的一个邻域内存在的话，那么 \(X\) 的任意一阶矩都存在，并且对于 \(k\in \bb N\)，我们有 \[ \E{X^k} = \dv[k]{}{t} M_X(0). \] 这个结论同时告诉我们，如果存在某个 \(m\in \bb N\)，使得 \(X^m\) 是不可积的，那么 \(M_X(t)\) 就不存在。但往往我们还是会对 \(k<m\) 时候 \(X\) 的 \(k\) 阶矩感兴趣，矩生成函数就无能为力了。这个时候就要小修改一下矩生成函数的定义。我们定义 \(X\) 的特征函数 \[ \varphi_X(t) \defeq \E{e^{i t X}}, \] 这儿 \(i=\sqrt{-1}\) 是虚数单位。注意到特征函数和矩生成函数唯一的不同是把 \(t\) 换成了 \(it\)。在 \(X\) 有概率密度 \(f(x)\) 的时候，它们分别对应了对 \(f(x)\) 的傅里叶变换和拉普拉斯变换。我们马上可以看到，\(\varphi_X(t)\) 总是存在的。

我们先来研究一下特征函数的一些基本性质。

根据欧拉公式 \[ \varphi_X(t) = \E{\cos tX} + i\E{\sin tX}. \] 由于 \(\sin\) 和 \(\cos\) 都是有界函数，因此可以看出 \(\varphi_X(t)\) 对于任意 \(t\) 都是存在的。这也是和 \(M_X(t)\) 的一个本质区别。
如果 \(X\) 存在密度函数 \(f_X(x)\)，那么 \[ \varphi_X(t) = \int_{-\infty}^\infty f_X(x)\cdot e^{itx} \d x \] 是 \(f_X(x)\) 的傅立叶变换。根据傅里叶逆变换定理， \[ f_X(x) = \lim_{T\to\infty} \int_{-T}^T \varphi_X(t)\cdot e^{-itx} \d t. \] 注意到对于这个不定积分我们使用了柯西主值，因为 \(\varphi_X(t)\) 不一定可积。这个结论告诉我们，密度函数唯一确定了特征函数，而特征函数也唯一确定了密度函数（也就是 \(X\) 的分布）。
上述结论可以被推广到一般的随机变量（当 \(X\) 不存在密度函数的情形），被称作 Lévy 逆定理。设 \(\bar F(x) = \frac{1}{2}\tp{F(x)+F(x-)}\)，其中 \(F(x-)\defeq \lim_{z\uparrow x} F(z)\)。那么 \[ \forall a<b,\quad \bar F(b) - \bar F(a) = \lim_{T\to\infty} \int_{-T}^T \frac{i}{2\pi t}\tp{e^{-ibt}-e^{-iat}}\cdot \varphi_X(t) \d t. \]

我们不会证明这个结论（证明可以查看上面链接），但强调一下 Lévy 逆定理说明了随机变量的分布和其特征函数是相互唯一对应的（当然了，如果两个分布只在一个零测集上不一样，我们也认为它们相同）。
根据定义容易验证，如果两个随机变量 \(X\) 和 \(Y\) 独立，那么 \(\varphi_{X+Y}(t) = \varphi_X(t)\cdot \varphi_Y(t)\)。类似的结论可以推广到 \(n\) 个相互独立的随机变量 \(X_1,\dots,X_n\)：\(\varphi_{\sum_{i=1}^n X_i}(t) = \prod_{i=1}^n \varphi_{X_i}(t)\)。

联合分布的特征函数

对于定义在同一个概率空间上的两个随机变量 \(X\) 和 \(Y\)，我们可以定义它们的联合特征函数 \[ \varphi_{(X,Y)}(s,t) = \E{e^{i\tp{sX+tY}}}. \] 这个定义可以推广到任意 \(n\) 个随机变量 \(\*X = (X_1,\dots,X_n)\)。它们的联合特征函数是 \[ \varphi_{\*X}\colon \*t\in \bb R^n \mapsto \E{e^{i\*t^\top \*X}}. \]

Lévy逆定理可以被推广到 \(\*X\) 这样的随机向量的场合。类似的，联合特征函数也唯一（up to 零测集）确定了联合分布。

特殊分布的特征函数计算

我们来给那几位老伙计算算特征函数。

\(X\sim\!{Ber}(p)\)

显然有 \(\varphi_X(t) = \E{e^{itX}} = 1-p+pe^{it}\).

\(X\sim\!{Binom}(n,p)\)

由于 \(X\) 可以写成 \(n\) 个分布为 \(\!{Ber}(p)\) 的独立随机变量之和，根据我们前面提到的性质，\(\varphi_X(t) = \tp{1-p+pe^{it}}^n\)。

\(X\sim\!{Exp}(\lambda)\)

由于指数分布的概率密度是 \(\forall x\ge 0,\;f_X(x) = \lambda e^{-\lambda x}\)，所以 \[ \varphi_X(t) = \E{e^{itX}} = \int_0^\infty \lambda e^{-\lambda x} e^{itx} \d x = \frac{\lambda}{\lambda-it}. \]

\(X\sim\!{Pois}(\lambda)\)

泊松分布的概率质量函数是 \(\forall n\in \bb N,\; p_X(n) = \frac{\lambda^n}{n!}e^{-\lambda}\)，所以 \[ \varphi_X(t) = \E{e^{itX}} = \sum_{n=0}^\infty \frac{\lambda^n}{n!}e^{-\lambda}e^{itn} = e^{-\lambda} \sum_{n=0}^\infty \frac{\tp{\lambda e^{it}}^n}{n!} = e^{-\lambda}e^{\lambda e^{it}}. \]

\(X\sim\+N(0,1)\)

标准高斯分布的概率密度是 \(\phi_X(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}\)，所以 \[ \varphi_X(t) = \E{e^{itX}} = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty e^{itx - \frac{x^2}{2}} \d x. \]
我们把积分里面的指数部分进行配方，然后做 \(z=x-it\) 的换元，可以得到 \[ \varphi_X(t) = \frac{e^{-\frac{t^2}{2}}}{\sqrt{2\pi}}\int_{\Im z = -t} e^{-\frac{1}{2}z^2} \d z. \] 这是一个在复平面上的积分，我们的积分范围是 \(\Im z = -t\) 的直线。对于给定的 \(N>0\)，我们计算如下图所示的围道积分。

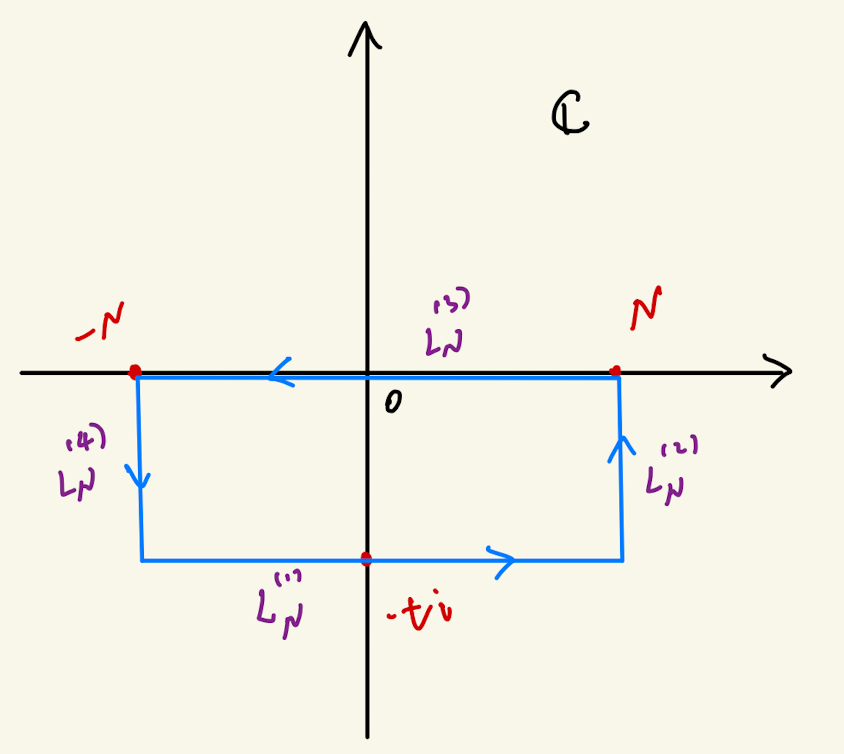
我们把蓝色曲线记作 \(L_N\)，那么根据柯西定理 \[ \int_{L_N} e^{-\frac{1}{2}z^2}\d z = \int_{L_N^{(1)}} e^{-\frac{1}{2}z^2}\d z + \int_{L_N^{(2)}} e^{-\frac{1}{2}z^2}\d z + \int_{L_N^{(3)}} e^{-\frac{1}{2}z^2}\d z + \int_{L_N^{(4)}} e^{-\frac{1}{2}z^2}\d z = 0. \]

注意到 \(\lim_{N\to\infty} \int_{L_N^{(2)}} e^{-\frac{1}{2}z^2}\d z = \lim_{N\to\infty} \int_{L_N^{(4)}} e^{-\frac{1}{2}z^2}\d z = 0\)，所以 \[ \lim_{N\to\infty} \int_{L_N^{(1)}} e^{-\frac{1}{2}z^2}\d z = -\lim_{N\to\infty} \int_{L_N^{(3)}} e^{-\frac{1}{2}z^2}\d z = \int_{-\infty}^\infty e^{-\frac{1}{2}z^2} \d z = \sqrt{2\pi}. \] 也就是说 \(\int_{\Im z = -t} e^{-\frac{1}{2}z^2}\d z = \sqrt{2\pi}\). 代回 \(\varphi_X(t)\) 的表达式我们便能得到 \[ \varphi_X(t) = e^{-\frac{t^2}{2}}. \] Wow，居然和 \(\phi_X(x)\) 的形式一致。高斯的傅里叶变换还是高斯。

\(X\sim\+N(\mu,\sigma^2)\)

如果 \(\xi\sim\+N(0,1)\)，那么 \(X\defeq \sigma \xi+\mu\sim \+N(\mu,\sigma^2)\)。根据定义，我们显然有 \[ \varphi_X(t) = \E{e^{it(\sigma \xi+\mu)}} = e^{it\mu}\E{e^{it\sigma\xi}} = e^{it\mu}\varphi_\xi(\sigma t) = e^{-\frac{\sigma^2t^2}{2}+it\mu}. \]

\(X\sim\+N\tp{\mu,\Sigma}\)

注意到这儿 \(X=(X_1,\dots,X_n)\) 是一个 \(n\) 维随机向量。我们计算它的联合特征函数。对于一个 \(\*t = (t_1,\dots,t_n)^\top\)，我们有 \[ \varphi_X(\*t) = \E{e^{i\*t^\top X}}. \] 我们注意到 \(Y\defeq \*t^\top X\) 是一个高斯随机变量，我们只要计算出 \(Y\) 的期望和方差，就能得到 \(Y\) 的特征函数 \(\varphi_Y(t)\)。而 \(\varphi_X(\*t) = \varphi_Y(1)\)。

我们显然有 \(\E{Y} = \*t^\top \E{X} = \*t^\top \mu\)。我们知道 \(X = A\xi+\mu\)，其中 \(\xi\sim\+N\tp{0,\!{Id}_n}\)，矩阵 \(A\) 满足 \(AA^\top = \Sigma\)。于是 \[ \Var{Y} = \E{\tp{\*t^\top A\xi}^2} = \*t^\top A\E{\xi\xi^\top} A^\top\*t = \*t^\top\Sigma\*t. \] 这便得到 \[ \varphi_X(\*t) = \varphi_Y(1) = e^{-\frac{1}{2}\*t^\top\Sigma\*t +i\*t^\top \mu}. \]

多元高斯分布的刻画

我们之前说一个 \(n\)-维随机变量 \(X=(X_1,\dots,X_n)^\top\) 是多元高斯（或称高维高斯，联合高斯）的，当且仅当存在 \(n\times n\) 维矩阵 \(A\) 和 \(n\) 维向量 \(\mu\) 使得 \(X = A\xi+\mu\)，其中 \(\xi\) 是一个每一维是独立 \(\+N(0,1)\) 随机变量的 \(n\) 维向量。并且我们知道 \(X\sim \+N\tp{\mu,\Sigma}\)，其中 \(\Sigma = AA^\top\)。我们现在给它一个新的刻画：

Theorem 1 \(X=(X_1,\dots,X_n)^\top\) 是一个高维高斯向量当且仅当 \(X_1,\dots,X_n\) 的任意线性组合是一个一维高斯随机变量。

定理的“仅当”方向是显然的，即如果 \(X\) 是高维高斯，那么 \(X_1,\dots,X_n\) 的任意线性组合也是高斯。这是由于每一个 \(X_i\) 都可以写成 \(\xi_1,\dots,\xi_n\) 的线性组合，于是任意 \(X_1,\dots,X_n\) 的线性组合也可以写成 \(\xi_1,\dots,\xi_n\) 的线性组合。而我们知道，独立高斯的线性组合依旧是高斯的。

我们现在来证明“当”。设 \(\mu = \E{X}\)，\(\Sigma = \Cov{X}\)。根据联合分布的 Lévy 逆定理，我们只要说明 \(X\) 的（联合）特征函数是高维高斯的就行。也就是对于任何 \(\*t\in \bb R^n\)，计算 \(\varphi_X(\*t) = \E{e^{i\*t^\top X}}\)。根据条件，我们知道 \(Y\defeq \*t^\top X\) 作为 \(X_1,\dots,X_n\) 的一个线性组合是满足高斯分布的。因此我们有 \(\varphi_X(\*t) = \varphi_Y(1)\)。同样我们只需要计算 \(Y\) 的期望和方差就能得到 \(\varphi_Y\)。 \[ \begin{align*} \E{Y} &= \*t^\top \E{X} = \*t^\top \mu,\\ \Var{Y} &= \E{\tp{\*t^\top X-\*t^\top\mu}^2} = \*t^\top\E{(X-\mu)(X-\mu)^\top}\*t = \*t^\top\Sigma\*t. \end{align*} \] 这便说明 \(\varphi_X(\*t) = \varphi_Y(1) = e^{-\frac{1}{2}\*t^\top\Sigma\*t +i\*t^\top \mu}\)。也就是说 \(X\sim \+N\tp{\mu,\Sigma}\)。

特征函数与随机变量的矩

我们在一开始便提到过，我们对矩生成函数求导可以得到随机变量的矩。但这一操作的可行性需要随机变量的任意一阶矩均存在。如果 \(X\) 对于 \(m\) 阶矩不存在，但对于 \(k<m\) 阶矩存在（回忆我们以前用 Jensen 不等式证明过对于 \(p>1\)，\(X^p\) 可积可以蕴含 \(X^{p-1}\) 可积），使用矩生成函数便不行了。下面这个结论，除了告诉我们可以使用特征函数来计算 up to \(m-1\) 阶矩之外，对于研究特征函数本身的性质有着重要的意义。

Theorem 2 如果随机变量 \(X\) 满足 \(\E{\abs{X}^n}<\infty\)，那么 \[ \varphi_X(t) = \sum_{k=0}^n \frac{(it)^k}{k!}\E{X^k} + o(\abs{t}^n). \] 特别的，对于 \(k=1,2,\dots,n\)，\(\dv[k]{}{t}\varphi_X(0) = i^k \E{X^k}\).

函数 \(e^{itX}\) 的泰勒级数的前 \(n\) 项是 \(\sum_{k=0}^n \frac{1}{k!}X^k(it)^k\)。因此，我们为了证明这个定理，需要讨论的事情主要是控制级数的余项，并据此说明可以交换求和和期望。

我们使用带有积分余项的泰勒级数： \[ f(z) = \sum_{k=0}^n \frac{f^{(k)}(0)}{k!}\cdot z^k + \frac{1}{n!}\int_0^z (z-t)^n f^{(n+1)}(t) \d t. \] 我们用 \(R_n\) 表示把 \(e^z\) 展开到 \(n\) 次之后的余项，于是 \[ e^{ix} = \sum_{k=0}^n \frac{(ix)^k}{k!} + R_{n+1},\quad R_{n+1} = \frac{i^{n+1}}{n!}\int_0^x (x-t)^n e^{it}\d t. \] 从这个表达式看起来，\(\abs{R_{n+1}} \le \frac{\abs{x}^{n+1}}{(n+1)!}\)。这在 \(x\to 0\) 的时候是一个很好的上界，但是我们的条件是 \(\E{\abs{X}^n}<\infty\)，在 \(x\to\infty\) 的时候 \(\abs{x}^{n+1}\) 太大了。我们需要找一个 \(x\to\infty\) 时更好的上界。注意到 \[ R_{n+1} = R_n - \frac{(ix)^n}{n!} = \frac{i^n}{n!}\tp{n\int_0^x (x-t)^{n-1} e^{it}\d t - x^n}. \] 于是 \(\abs{R_{n+1}}\le \frac{2\abs{x}^n}{n!}\)。我们便得到了 \[ \abs{R_{n+1}}\le \frac{\abs{x}^{n+1}}{(n+1)!}\land \frac{2\abs{x}^n}{n!}. \] 根据条件 \(\E{\abs{X}^n}<\infty\)，我们知道 \[ e^{itX} = \sum_{k=0}^n \frac{(itX)^k}{k!} + R_{n+1}'(X), \quad \abs{R_{n+1}'(X)} \le \frac{2\abs{t}^n\abs{X}^n}{n!} \] 满足求和的每一项都是可积的。因此，根据期望的线性性，我们有 \[ \E{e^{itX}} = \sum_{k=0}^n \frac{(it)^k}{k!}\E{X^k} +\E{R_{n+1}'(X)}. \] 我们接着说明 \(\E{\abs{R_{n+1}'(X)}} = o(\abs{t}^n)\) as \(t\to 0\)。这等价于 \(\lim_{t\to 0} t^{-n}\E{\abs{R_{n+1}'(X)}} = 0\)。根据我们上面的对于余项的上界可以知道 \(t^{-n} \abs{R_{n+1}'(X)}\le \frac{2\abs{X}^n}{n!}\). 因此使用 DCT， \[ \lim_{t\to 0} t^{-n}\E{\abs{R_{n+1}'(X)}} = \E{\lim_{t\to 0}t^{-n}\abs{R_{n+1}'(X)}}\le \E{\lim_{t\to 0}\frac{t\abs{X}^{n+1}}{(n+1)!}} = 0. \]

注意到我们在上面的分析中，同时用到了 \(R_{n+1}\) 的两个上界，分别对应于 \(x\) 很大和 \(x\) 很小的时候。

Lévy 连续性定理及应用

特征函数的另一个重要性质说的是它与依分布收敛的关系。我们不加证明的给出结论

Theorem 3 (Lévy 连续性定理) 给定一族（不一定定义在同一概率空间上的）随机变量 \(X_1,X_2,\dots\)。对于每一个 \(n\ge 1\)，我们用 \(\varphi_n\) 表示 \(X_n\) 的特征函数。如果 \(\varphi_n(t)\) 逐点收敛到一个函数 \(\varphi(t)\)。那么下面两件事情等价。

\(\varphi(t)\) 在 \(t=0\) 连续；
存在一个随机变量 \(X\)，它的特征函数是 \(\varphi\)，并且 \(X_n\overset{D}{\to} X\)。

另一方面，我们可以很容易验证，如果 \(X_n\overset{D}{\to} X\)，那么 \(\varphi_n(t)\) 逐点收敛到 \(\varphi(t)\) （类似我们之前用测试函数说明依分布收敛的证明，这儿对应的测试函数是 \(h_t(x) = e^{itx}\) ）。所以，我们知道，在 \(\varphi(t)\) 在 \(t=0\) 连续的条件下，依分布收敛和特征函数的逐点收敛是等价的。

我们简单说明一下，\(\varphi(t)\) 在 \(t=0\) 这一点连续的条件是必要的，否则 \(\varphi(t)\) 有可能并不是任何函数的特征函数。比如说，我们让 \(X_n\sim\+N(0,n)\)，那么 \(\varphi_n(t) = e^{-\frac{nt^2}{2}}\)。它的极限是 \(\varphi(t) = \bb I[t=0]\)，在 \(t=0\) 不连续，也不是任何随机变量的特征函数。

Lévy 连续定理是我们研究依分布收敛的重要工具。接下来我们看几个应用。

泊松分布作为二项式分布的极限

我们之前介绍泊松分布 \(\!{Pois}(\lambda)\) 的时候是把它看成二项式分布 \(\!{Binom}(n,p)\) 在 \(np = \lambda\) 时候的极限。这个事实可以用特征函数一句话说明。注意到 \(X\sim\!{Binom}(n,p)\) 的特征函数是 \[ \tp{1-p+pe^{it}}^n = \tp{1-\frac{np-np e^{it}}{n}}^n = \tp{1-\frac{\lambda-\lambda e^{it}}{n}}^n\overset{n\to\infty}{\to} e^{-\lambda} e^{\lambda e^{it}}. \] 而这正是 \(\!{Pois}(\lambda)\) 的特征函数。

中心极限定理的特征函数证明

我们现在用特征函数来证明中心极限定理。

Theorem 4 (中心极限定理) 如果独立同分布的随机变量 \(X_1,X_2,\dots\) 满足 \(\E{X_1}=\mu, \Var{X_1}=\sigma^2\) 均为有限的，那么 \[ \frac{S_n-n\mu}{\sigma\sqrt{n}}\overset{D}{\to} Y\sim\+N(0,1). \]

我们不失一般性的假设 \(\mu=0\), \(\sigma^2=1\)。我们已经证明了 \[ \varphi_{X_1}(t) = \E{e^{itX_1}} = \E{1+itX_1-\frac{1}{2}t^2X_1^2+\eps(t^2)} = 1-\frac{1}{2}t^2+\eps(t^2). \] 这儿 \(\eps(t)\) 是一个满足 \(\lim_{t\to 0} \frac{\eps(t)}{t} = 0\) 的函数。于是根据独立性 \[ \varphi_{\frac{S_n}{\sqrt{n}}}(t) = \varphi_{X_1}\tp{\frac{t}{\sqrt{n}}}^n = \tp{1-\frac{t^2}{2n}+\eps\tp{\frac{t^2}{n}}}^n\overset{n\to\infty}{\to} e^{-\frac{1}{2}t^2}. \] 由 Lévy 连续性定理 \(\frac{S_n}{\sqrt{n}}\overset{D}{\to}\xi\sim\+N(0,1)\)。

可以看到，特征函数是处理独立随机变量和的有力工具。我们将在作业里尝试使用它去掉 CLT 里对于同分布的要求。