第二十八讲：可选停时定理

回忆我们上节课介绍过的离散鞅的概念。固定概率空间 \((\Omega,\@F,\bb P)\) 以及上面的一个滤链 \(\set{\@F_t}_{t\ge 0}\)。我们说一族可积的随机变量 \(\set{X_t}_{t\ge 0}\) 是相对于 \(\set{\@F_t}_{t\ge 0}\) 的鞅当且仅当 \[ \forall t\ge 0,\;\E{X_{t+1}\mid\@F_t} = X_t. \] 对于每一个 \(t\ge 0\)，我们对上式两边同时取期望并使用 tower rule，可以得到 \(\E{X_{t+1}} = \E{X_t}\)。换句话说，对于每一个固定的 \(t\)，我们都有 \(\E{X_t}=\E{X_0}\) 成立。但我们现在假设 \(\tau\) 是一个随机的时间，是一个随机变量，\(\E{X_\tau}=\E{X_0}\) 依然成立吗？答案是不一定，我们可以看下面这个例子：

考虑一个公平游戏中的如下赌博策略。在第一轮中，赌徒下注 \(1\) 元。然后，他简单地将赌注翻倍，直到他赢得游戏（有趣的是，这个赌博策略也被称为 martingale）。如果我们用 \(Z_t\) 表示他 \(t\) 轮之后赢得的金额，在上节课我们已经知道 \(\set{Z_t}_{t\ge 0}\) 是一个鞅。令 \(\tau\) 表示他第一次赢得游戏的时间。首先我们知道 \(\Pr{\tau<\infty}=1\)。注意到

如果 \(\tau = 1\)，他赢得 1 元。
如果 \(\tau = 2\)，他赢得 \(-1 + 2 = 1\) 元。
如果 \(\tau = 3\)，他赢得 \(-1 - 2 + 4 = 1\) 元。
…

他在赢得游戏的时候一定是赢得 \(1\) 元钱。也就是说 \(\E{Z_\tau} = 1\ne \E{Z_0} = 0\)。我们马上会看到，理解在什么时候 \(\E{Z_\tau}=\E{Z_0}\) 是一件很重要的事情。

可选停时定理（Optional Stopping Theorem）

我们首先要定义停时（stopping time）的概念。

Definition 1 (停时) 设 \(\set{\@F_t}_{t\ge 0}\) 是概率空间 \((\Omega,\@F,\bb P)\) 上的一个滤链。我们说取值为自然数的随机变量 \(\tau\colon \Omega\to\bb N\) 为一个停时，当且仅当对于任何 \(t\in \bb N\)，事件 \([\tau\le t]\) 是 \(\@F_t\)-可测的。

我们有的时候也会说 \(\tau\) 是关于 \(X_0,X_1,\dots\) 的停时，这个时候的意思是在上面的定义里取 \(\@F_i = \sigma\tp{X_0,\dots,X_i}\)。

直观上说，如果想象在玩一个一轮又一轮的游戏，\(\@F_t\) 表示前 \(t\) 轮所有的信息。那么 \(\tau\) 是一个停时的意思是在每一轮游戏结束后，玩家应该就有足够的信息判断是否应该在此时结束游戏了。举个例子，我们平时晚上打游戏的时候经常说的“赢一把就睡”就是一个停时，但比如“今晚赢的最多的一局后结束”就不是一个停时，因为在当前你不知道这一局是不是赢得最多的一局。

假设 \(\set{X_t}_{t\ge 0}\) 是相对于 \(\set{\@F_t}_{t\ge 0}\) 的鞅，\(\tau\) 是一个停时。可选停时定理给出了 \(\E{X_\tau} = \E{X_0}\) 成立的几个充分条件。我们将在今天最后证明这个定理。从这个定理的证明中也容易看出来，\(\E{X_\tau}=\E{X_0}\) 成立的本质原因是什么样的。

Theorem 1 (可选停时定理（Optional Stopping Theorem, OST）) 如果以下任意一个条件成立，则 \(\E{X_\tau} = \E{X_0}\)：

[OST1] \(\tau\) almost surely 有界，也就是说，存在某个 \(n \in \bb N\) 使得 \(\Pr{\tau \leq n} = 1\)； [OST2] \(\Pr{\tau < \infty} = 1\) ，且存在有限的 \(M\)，使得 \(|X_t| \leq M\) 对于所有 \(t \le \tau\) 成立； [OST3] \(\E{\tau} < \infty\)，且存在一个常数 \(c\)，使得 \(\E{|X_{t+1} - X_t| \mid \@F_t} \leq c\) almost surely 对于所有 \(t \le \tau\) 成立。

我们之后会用 OST 来简称可选停时定理，会用 [OST1], [OST2], [OST3] 来分别指代我们使用 OST 的时候验证的充分条件。值得注意的是，[OST2] 里面的要求 \(\Pr{\tau<\infty}=1\) 是比 [OST3] 里面的 \(\E{\tau}<\infty\) 要更弱的条件，但作为代价， \(\abs{X_t}\) 有界是比 \(\E{\abs{X_{t+1}-X_t} \mid \@F_t}\) 有界更强的条件。在具体应用中，我们要根据需要选择合适的条件。

首先来看一个耳熟能详的例子。假设有一个村庄，那儿的人重男轻女。那么在以下三种情况下，长期来看该村庄的性别比例是多少？

每个家庭持续生育，直到他们生了一个男孩。
每个家庭持续生育，直到男孩的数量多于女孩。
每个家庭持续生育，直到男孩的数量多于女孩或孩子总数达到 10。

我们可以将问题建模为一个随机游走。假设有一个人在一维整数轴上随机游走。令 \(\{X_t\}_{t \geq 0}\) 表示每个时间点上的位置，其中 \(X_t\) 表示一个家庭在前 \(t\) 个孩子中男孩数量减去女孩数量。初始时 \(X_0 = 0\)，在时间 \(t=0\) 时，该人向 \(c_t \in \{-1, 1\}\) 方向随机迈出一步，到达 \(X_{t+1}\)，即 \(X_{t+1} = X_t + c_t\)。很容易验证 \(\{X_t\}_{t \geq 0}\) 是一个鞅。

上述三种情况对应于停止时间 \(\tau\) 的三种不同定义。我们可以简单的认为 \(\E{X_\tau} = \E{X_0}\) 表明性别比例是平衡的。我们分别检查这些情况是否满足 OST。

【\(\tau\) 是 \(c_t = 1\) 的第一次出现的时间】在这种情况下，由于 \(\tau\sim\!{Geom}\tp{\frac{1}{2}}\)，所以 \(\E{\tau} = \frac{1}{2}<\infty\)。并且 \(|X_{t+1} - X_t| \leq 1\) 对于所有 \(t < \tau\) 成立。因此，根据 [OST3]，我们有 \(\E{X_\tau} = \E{X_0} = 0\)。换句话说，如果人在 \(c_t = 1\) 第一次出现时停止，那么他停止的位置的期望是 \(0\)。
【\(\tau\) 是 \(X_t = 1\) 的第一次出现的时间】在这种情况下，显然 \(\E{X_\tau} = 1 \neq \E{X_0}\)。这个过程被称为“一维随机游走的单吸收屏障问题”。容易证明（使用递推），\(\Pr{\tau<\infty}=1\) 但是 \(\E{\tau} = \infty\)，没有任何一个 OST 条件被满足。在随机过程里，这个性质被称为“零返性”
【\(\tau\) 是 \(t = 10\) 和 \(X_t = 1\) 中最早发生的那个 \(t\)】在这种情况下，\(\tau\) 至多为 10，满足 [OST1]。因此我们有 \(\E{X_\tau} = \E{X_0} = 0\)。

可选停时定理的应用

我们接下来介绍可选停时定理的一些经典应用，可以从中瞥见其威力。

Doob的鞅不等式

通过可选停时定理，我们可以获得随机变量序列中最大值的集中性质。

Lemma 1 (Doob的鞅不等式) 令 \(\{X_t\}_{t \geq 0}\) 是一个关于自身的鞅，且对于每个 \(t\) 都有 \(X_t \geq 0\)。那么对于任何 \(n \in \bb N\) 和 \(\alpha > 0\)，有： \[ \Pr{\max_{0 \leq t \leq n} X_t \geq \alpha} \leq \frac{\E{X_0}}{\alpha}. \]

注：如果我们把引理里面的鞅改成下鞅，则不等式右边的 \(\E{X_0}\) 可以换成 \(\E{X_n \lor 0}\)。这个的证明我们留作练习。

Proof. 定义停时 \(\tau\) 为第一次出现大于 \(\alpha\) 的 \(X_t\) 所对应的 \(t\)。如果不存在这样的 \(t\)，则令 \(\tau = n\)。即： \[ \tau \defeq \min \left\{n, \min_{0 \leq t \leq n} \set{t \mid X_t \geq \alpha}\right\}. \]

根据 \(\tau\) 的定义，有： \[ \Pr{\max_{0 \leq t \leq n} X_t \geq \alpha} = \Pr{X_\tau \geq \alpha}. \]

由于 \(\tau\) 有界（\(\tau \leq n\)），[OST1] 成立，于是有 \(\E{X_\tau} = \E{X_0}\)。使用马尔科夫不等式便得到 \[ \Pr{X_\tau \geq \alpha} \leq \frac{\E{X_\tau}}{\alpha} = \frac{\E{X_0}}{\alpha}. \]

具有两侧吸收壁的一维随机游走

设 \(a, b > 0\) 为两个正整数。一个人从位置 \(0\) 开始随机游走，每次等概率往左或者往右移动距离 \(1\)。当他到达 \(-a\) 或 \(b\) 时停止。令 \(\tau\) 表示他第一次到达 \(-a\) 或 \(b\) 的时间，即 \(\tau=\min\set{t\ge 0\cmid X_t = -a \lor X_t = b}\)。显然 \(\tau\) 是一个停时。该模型被称为一维随机游走的双吸收屏障问题。我们希望计算 \(\E{\tau}\)，即平均停止时间。

我们首先来计算 \(\Pr{X_\tau = -a}\)，即该人停在位置 \(-a\) 的概率。令 \(P_a \defeq \Pr{X_\tau = -a}\)。我们希望通过 OST 证明 \(\E{X_\tau} = \E{X_0}\)。为此，我们验证 OST 的几个条件。

首先 [OST1] 在 \(a\), \(b\) 不同时是 \(1\) 的时候显然不成立。
我们可以验证更强的条件 \(\E{\tau}<\infty\) 是成立的。我们使用一个基于耦合的证明。想象我每 \((a+b)\) 步投掷一枚 \(\!{Ber}\tp{2^{-(a+b)}}\) 的硬币。如果硬币是正面，就想象我在接下来的 \(a+b\) 步里一直往右走。如果这件事情发生，那我在未来 \(a+b\) 步内一定会停止。因此，我停止的时间 \(\tau\) 可以被一个 \(\!{Geom}\tp{2^{-(a+b)}}\) 的随机变量乘上 \((a+b)\) 给控制住。因此 \(\E{\tau}\le (a+b)\cdot 2^{a+b}\)。此外，显然对于每个 \(0 \leq t \le \tau\)，都有 \(\E{\abs{X_{t+1} - X_t} \mid \@F_t} \leq 1\)，所以根据 [OST3]，\(\E{X_\tau} = \E{X_0} = 0\)。

另一方面，我们有 \(\E{X_\tau} = P_a \cdot (-a) + (1 - P_a) \cdot b\)。结合 \(\E{X_\tau} = \E{X_0} = 0\)，我们有 \(P_a = \frac{b}{a + b}\)。

我们接下来计算 \(\E{\tau}\)。对于每个 \(t \geq 0\)，我们定义一个新的随机变量 \(Y_t \defeq X_t^2 - t\)。我们可以通过定义验证 \(\set{Y_t}_{t\ge 0}\) 是一个鞅：

\[ \forall t\ge 0,\; \E{Y_{t+1} \mid \@F_t} = \E{X_{t+1}^2 - (t + 1) \mid \@F_t}. \] 根据 \(X_{t+1} = X_t + c_t, \;c_t \in \{-1, 1\}\)，有 \(X_{t+1}^2 = (X_t + c_t)^2 = X_t^2 + 2X_t c_t + c_t^2\)。代入后得到 \[ \E{Y_{t+1} \mid \@F_t} = \E{X_t^2 + 2X_t c_t + c_t^2 - (t + 1) \mid \@F_t}. \]

由于 \(X_t\) 是 \(\@F_t\)-可测的，且 \(\E{c_t \mid \@F_t} = 0\)，\(\E{c_t^2 \mid \@F_t} = 1\)。因此 \[ \E{Y_{t+1} \mid \@F_t} = X_t^2 + 0 + 1 - (t + 1) = X_t^2 - t = Y_t. \]

注意 \(X_t \in [-a, b]\)，因此对于所有 \(t\le\tau\)，\(|Y_{t+1} - Y_t|\) 是有界的，满足 [OST3]。我们使用 OST 得到 \[ \E{Y_\tau} = \E{Y_0} = 0. \]

另一方面，由 \(Y_t\) 的定义，有 \(\E{Y_\tau} = \E{X_\tau^2} - \E{\tau}\)。因此 \(\E{\tau} = \E{X_\tau^2}\)。我们知道： \[ \E{X_\tau^2} = P_a \cdot (-a)^2 + (1 - P_a) \cdot b^2. \] 代入 \(P_a = \frac{b}{a + b}\)，得到： \[ \E{\tau} = \E{X_\tau^2} = \frac{b}{a + b} \cdot a^2 + \frac{a}{a + b} \cdot b^2 = ab. \]

模式的期望出现时间

假设有一个由 \(\set{\!H, \!T}\) 组成的字符串 \(P\) （称为模式串），长度为 \(\ell\)（\(\!H\) 表示“正面”，\(\!T\) 表示“反面”）。我们连续抛掷硬币，直到最后的 \(\ell\) 次结果形成一个与 \(P\) 完全相同的字符串。我们希望计算需要抛掷硬币的期望次数。

首先，如果我们抛掷硬币 \(N\) 次，并观察结果字符串 \(S\)。根据期望的线性性，无论 \(P\) 是什么，它在字符串 \(S\) 中的期望出现次数为 \[ \E{\#\text{ of occurrences of } P \text{ in } S} = \sum_{i=1}^{n-\ell+1} \E{\bb I_{S_{i,i+1,\dots,i+\ell-1} = P}} = (n - \ell + 1) \cdot 2^{-\ell}. \] 也就是说，不管 \(P\) 是什么，它期望出现的次数总是一定的。但如果我们考虑第一次出现 \(P\) 的平均时间，就会有所不同。比如说，我们考虑以下两种模式串 \(\!H\!T\) 和 \(\!H\!H\):

假设第一次抛掷结果是 \(\!H\)。如果第二次抛掷失败：
- 如果目标模式是 \(\!H\!T\)，那么尽管失败了，我们仍然得到了一个 \(\!H\)，模式串的第一位被匹配上了。
- 如果目标模式是 \(\!H\!H\)，第二次抛掷结果是 \(\!T\)，那么我们什么都没有得到，前两次抛掷的结果完全浪费。

因此，直观上我们应该相信，模式串 \(\!H\!T\) 的第一次出现的期望时间比 \(\!H\!H\) 更小。我们接下来严格的说明这件事情。

令模式 \(P = p_1p_2 \dots p_\ell\)。对于每个 \(n \geq 0\)，假设在第 \(n+1\) 次抛掷之前，有一个新的赌徒 \(G_{n+1}\) 带着 1 单位的资金下注，赌接下来的 \(\ell\) 次结果（即第 \(n+1\) 到 \(n+\ell\) 次结果）完全和 \(P\) 相同。换句话说，在第 \(n+k\) 次抛掷时，赌徒 \(G_{n+1}\) 会采用全押策略下注第 \(n+k\) 次的结果是 \(p_k\)：

如果第 \(n+k\) 次结果是 \(p_k\)，赌徒的资金会翻倍；
否则，赌徒会输掉所有资金。

假设 \(P = \!{HTHTH}\)，抛掷结果为 \(\!{HTHHTHTH}\)。下表展示了每位赌徒在每次抛掷后的总资金：

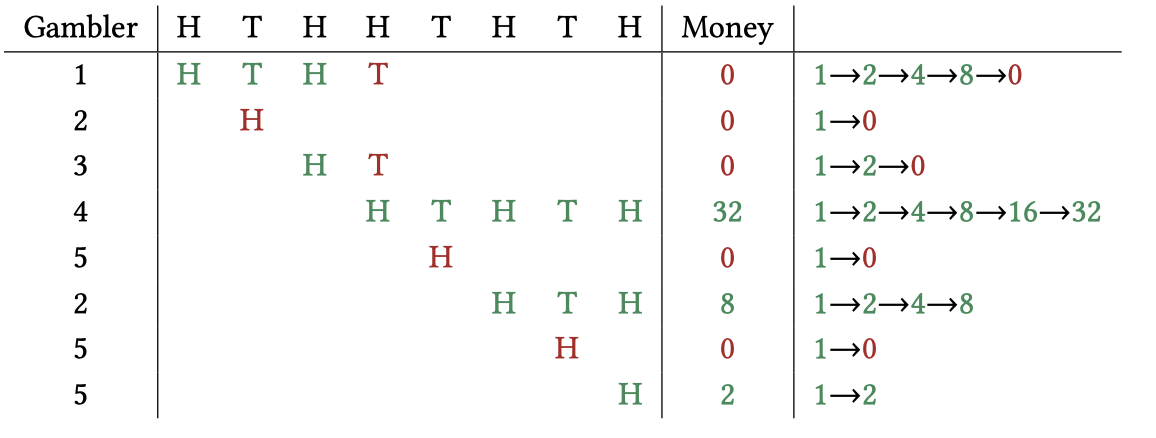
令 \(X_t\) 表示第 \(t\) 次抛掷的结果，\(M_i(t)\) 表示赌徒 \(G_i\) 在第 \(t\) 次抛掷后的资金，定义：

\[ Z_t\defeq \sum_{i=1}^t \tp{M_i(t) - 1}, \]

即在第 \(t\) 次抛掷后，所有赌徒的总收入。可以验证对于每一个 \(i\)，\(\{M_i(t)\}_{t \geq 0}\) 是一个关于抛掷结果 \(\{X_t\}_{t\ge 1}\) 的鞅：

\[ \E{M_i(t+1) \mid \ol{X}_{1,t}} = \frac{1}{2} \cdot 2M_i(t) + \frac{1}{2} \cdot 0 = M_i(t). \]

根据期望的线性性，我们也可以得到 \(\{Z_t\}_{t \geq 0}\) 是一个鞅。令 \(\tau\) 表示第一次某个赌徒赢得比赛的时间，即模式串 \(P\) 首次被掷出的时间。我们容易验证 [OST3] 是满足的（why？）。于是，\(\E{Z_\tau} = \E{Z_0} = 0\)。因此，我们得到 \[ \E{\sum_{i=1}^\tau M_i(\tau) - \tau} = 0, \] 期望里的两项都是可积的（why？），于是根据期望的线性性，我们有 \[ \E{\tau} = \E{\sum_{i=1}^\tau M_i(\tau)}. \] 注意到对于 \(i \leq \tau - \ell\)，\(M_i(\tau) = 0\)，而对于 \(i > \tau - \ell\)，有 \[ M_i(\tau) = 2^{\tau - i + 1} \chi_{\tau - i + 1}, \] 其中 \(\chi_j = \bb I_{[p_1p_2 \dots p_j = p_{\ell - j + 1} \dots p_\ell]}\)。因此 \(\E{\tau} = \sum_{i=1}^\ell 2^i \chi_i\)。

我们对 \(\!{HH}\) 和 \(\!{HT}\) 来做一个 sanity check。

如果 \(P=\!{HH}\)，那么 \(\E{\tau} = 2 + 4 = 6\)。
如果 \(P=\!{HT}\)，那么 \(\E{\tau}= 4\)。

这验证了我们之前的直观：\(\!{HH}\) 的第一次出现的期望时间比模式 \(\!{HT}\) 更大。

Wald 等式

在实际中，我们经常需要分析如下过程的（期望）运行时间，其中 cond 和 compute() 都是随机的：

while cond do
    compute();
end while

假设第 \(i\) 次调用 compute() 的耗时为 \(X_i\)，算法在经过 \(T\) 次迭代后终止（ \(T\) 有可能是随机的）。那么总运行时间为 \(N \defeq \sum_{i=1}^{T} X_i\)。我们现在想来计算 \(\E{N}\)。

Theorem 2 (Wald 等式) 如果以下条件成立

\(X_1, X_2, \dots\) 是非负的、独立的可积随机变量，并且期望均为 \(\mu\)；
\(T\) 是 \(X_1, X_2, \dots\) 的停时；
\(\E{T} < \infty\)。

那么就有 \(\E{\sum_{i=1}^T X_i} = \E{T} \cdot \mu\) 成立。

Proof. 对于 \(i \geq 1\)，定义随机变量 \[ Z_i \defeq \sum_{j=1}^i \tp{X_j - \mu}. \] 显然，序列 \(\{Z_i\}_{i \geq 1}\) 是关于 \(X_1, X_2, \dots\) 的鞅，并且 \(\E{Z_1} = 0\)。同时，我们有以下等式： \[ \E{|Z_{i+1} - Z_i| \mid \@F_i} = \E{\abs{X_{i+1} - \mu} \mid \@F_i} \leq \E{X_{i+1} + \mu \mid \@F_i} \leq 2\mu. \] 我们知道 \(\E{T} < \infty\)，因此满足 [OST3]，所以 \(\E{Z_T} = \E{Z_1} = 0\)。于是 \[ \E{Z_T} = \E{\sum_{j=1}^T (X_j - \mu)} = \E{\sum_{j=1}^T X_j} - \E{T} \cdot \mu = 0. \] 由此可得 \(\E{\sum_{j=1}^T X_j} = \E{T} \cdot \mu\)。

Wald等式的应用：一个路由问题

我们来看一个 Wald 等式的应用。如下图所示，假设有 \(n\) 个发送者和一个接收者。在每一轮中，每个发送者以概率 \(\frac{1}{n}\) 向接收者发送一个数据包。由于所有发送者共享同一个信道，如果有多个数据包同时被发送，则所有数据包都会失败。

我们的问题是，每个发送者至少成功发送一个数据包所需的平均轮次是多少？

令 \(X_i\) 为接收者在成功接收到第 \(i-1\) 个数据包后，再次成功接收到一个数据包所需的轮数。令 \(T\) 表示接收者第一次成功收到每个发送者至少一个数据包所需的数据包总数。那么我们感兴趣的总时间为： \[ N \defeq \sum_{i=1}^T X_i. \]

显然，\(X_1, X_2, \dots\) 是独立同分布的，且 \(\E{T}\) 有界。因此，根据 Wald 等式有 \(\E{N} = \E{T} \cdot E[X_1]\)。注意到根据定义，\(T\) 是奖券收集问题中收集全一套所需要的开包总数，因此 \(\E{T} = nH_n = \Theta(n \log n)\)。另一方面，\(X_1\) 服从几何分布 \(\!{Geom}(p)\)，其中 \[ p = n \cdot \frac{1}{n} \left(1 - \frac{1}{n}\right)^{n-1} \approx e^{-1}. \] 所以 \(\E{X_1} = \frac{1}{p} = e\)。我们最终得到 \(\E{N} = \E{T}\cdot\E{X_1}\approx e\cdot nH_n\)。

可选停时定理的证明

我们重述一下 OST 并证明之。

如果以下任意一个条件成立，则 \(\E{X_\tau} = \E{X_0}\)：

[OST1] \(\tau\) almost surely 有界，也就是说，存在某个 \(n \in \bb N\) 使得 \(\Pr{\tau \leq n} = 1\)；
[OST2] \(\Pr{\tau < \infty} = 1\) ，且存在有限的 \(M\)，使得 \(|X_t| \leq M\) 对于所有 \(t \le \tau\) 成立；
[OST3] \(\E{\tau} < \infty\)，且存在一个常数 \(c\)，使得 \(\E{|X_{t+1} - X_t| \mid \@F_t} \leq c\) almost surely 对于所有 \(t \le \tau\) 成立。

首先我们可以不失一般性的把 almost surely 去掉，因为在零测集上的取值并不影响期望。然后我们注意到，对于每一个 \(n \in \bb N\)，鞅的性质保证了 \(\E{X_n} = \E{X_0}\)。接下来，我们证明对于任意 \(n \in \mathbb{N}\)，有 \(\E{X_{\tau\land n}} = \E{X_0}\) 成立。为了说明这个，我们定义 \[ \forall n\ge 0,\;Z_n \defeq X_{n\land \tau} = X_0 + \sum_{i=0}^{n-1} \tp{X_{i+1} - X_i}\bb I_{[i<\tau]}. \] 我们接着验证 \(\{Z_n\}_{n \geq 0}\) 是一个鞅。根据定义 \[ \E{Z_{n+1} \mid \@F_n} = \E{Z_n + \tp{X_{n+1} - X_n}\bb I_{[n<\tau]} \mid \@F_n}. \] 由于 \([\tau > n]\) 是 \(\@F_n\)-可测的，且 \(\E{X_{n+1} \mid \@F_n} = X_n\)，我们有 \[ \E{Z_{n+1} \mid \@F_n} = Z_n + \bb I_{[n < \tau]} \cdot \tp{\E{X_{n+1} \mid \@F_n} - X_n} = Z_n. \] 因此，\(\{Z_n\}_{n \geq 0}\) 是一个鞅。所以 \[ \E{X_{\tau\land n}} = \E{Z_n} = \E{Z_0} = \E{X_0}. \] 上述讨论促使我们把 \(X_\tau\) 分解成以下两部分： \[ X_\tau = X_{\tau\land n} + \bb I_{[n < \tau]} \cdot (X_\tau - X_n). \] 对两边取期望并令 \(n \to \infty\)，得到： \[ \E{X_\tau} = \E{X_0} + \lim_{n \to \infty} \E{\bb I_{[n<\tau]} \cdot (X_\tau - X_n)}. \]

因此，我们只需验证 [OST1], [OST2], [OST3] 都能保证保证 \(\lim_{n \to \infty} \E{\bb I_{[n<\tau]} \cdot (X_\tau - X_n)} = 0\)。

[OST1]

如果 \(\tau\) 几乎必然有界，则存在某个 \(n\) 使得 \(\Pr{\tau \leq n} = 1\)。因此，对于足够大的 \(n\)，有： \[ \E{\bb I_{[n < \tau]} \cdot (X_\tau - X_n)} = 0. \]

[OST2]

在这种情况下： \[ \E{\bb I_{[n<\tau]} \cdot (X_\tau - X_n)} \leq \E{\bb I_{[n<\tau]} \cdot \tp{|X_\tau| + |X_n|}}. \] 由于 \(\abs{X_t} \leq M\) 对于所有 \(t < \tau\) 成立，因此： \[ \E{\bb I_{[n <\tau]} \cdot \tp{|X_\tau| + |X_n|}} \leq 2M \cdot \Pr{\tau > n}. \] 而当 \(n \to \infty\) 时，\(\Pr{\tau > n} \to 0\)。

[OST3]

在这种情况下，我们要利用 \(X_t\) 之间的增量有界。于是 \[ \begin{align*} \bb I_{[n<\tau]} \cdot (X_\tau - X_n) &= \sum_{t=n}^{\tau-1} \tp{X_{t+1} - X_t} \le \sum_{t=n}^{\tau-1}\abs{X_{t+1}-X_t} =\sum_{t=n}^\infty \abs{X_{t+1}-X_t}\cdot \bb I_{[\tau>t]}. \end{align*} \] 对两边取期望，并使用 MCT，可以得到 \[ \E{\bb I_{[n<\tau]}\cdot (X_\tau-X_n)} \le \E{\sum_{t=n}^\infty \abs{X_{t+1}-X_t}\cdot \bb I_{[\tau>t]}} = \sum_{t=n}^\infty \E{\abs{X_{t+1}-X_t}\cdot \bb I_{[\tau>t]}}. \] 使用 tower rule，并注意到 \(\bb I_{[\tau>t]}\) 是 \(\@F_t\)-可测的，我们知道对于任何 \(t\ge n\) 有 \[ \E{\abs{X_{t+1}-X_t}\cdot \bb I_{[\tau>t]}} = \E{\E{\abs{X_{t+1}-X_t}\cdot \bb I_{[\tau>t]}\mid \@F_t}} = \E{\E{\abs{X_{t+1}-X_t}\mid \@F_t}\cdot \bb I_{[\tau>t]}}. \] 根据 [OST3]，对于 \(t\le \tau\)，\(\E{\abs{X_{t+1}-X_t}\mid \@F_t}\le c\)，我们有 \[ \sum_{t=n}^\infty \E{\abs{X_{t+1}-X_t}\cdot \bb I_{[\tau>t]}}\le \sum_{t=n}^\infty c\cdot\Pr{\tau >t}. \] 我们又知道 \(\E{\tau} = \sum_{t=0}^\infty \Pr{\tau >t} <\infty\)。因此上式在 \(n\to\infty\) 的时候是一个有限级数的 tail，所以收敛到零。